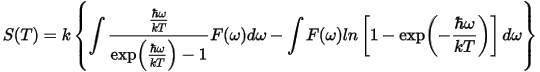Thermodynamic calculations
The results of a calculation of phonon spectra can be used to compute energy (E), entropy (S), free energy (F), and lattice heat capacity (Cv) as functions of temperature. The CASTEP total energy yields the total electronic energy at 0 K. The vibrational contributions to the thermodynamic properties are evaluated to compute E, S, F, and Cv at finite temperatures as discussed below.
Thermodynamic calculations can be performed only if the system is in the ground state, that is, geometry optimization is fully converged. This means that all the phonon eigenfrequencies must be real and non-negative.
When you perform a vibrational analysis with CASTEP the results of the thermodynamic calculations can be visualized using the thermodynamic analysis tools.
The formulas below are based on work by Baroni et al. (2001).
The temperature dependence of the energy is given by:
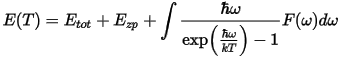
where Ezp if the zero point vibrational energy, k is the Boltzmann constant, ħ is the Planck constant and F(ω) is the phonon density of states. Ezp can be evaluated as:
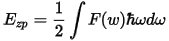
The vibrational contribution to the free energy, F, is given by:
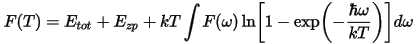
The lattice contribution to the heat capacity, Cv, is:
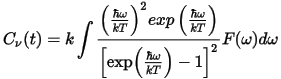
A popular representation of the experimental data on heat capacity is based on the comparison of the actual heat capacity to that predicted by the Debye model. This leads to the concept of the temperature dependent Debye temperature, ΘD(T). Heat capacity in Debye model is given by (Ashcroft and Mermin, 1976):
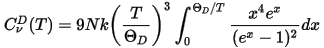
where N is the number of atoms per cell. Thus, the value of the Debye temperature, ΘD, at a given temperature, T, is obtained by calculating the actual heat capacity, Eq. CASTEP 84, then inverting Eq. CASTEP 85 to obtain ΘD.