Linear response
Linear response, or density functional perturbation theory (DFPT), is one of the most popular methods of ab initio calculation of lattice dynamics (Baroni et al. 2001). However, the applicability of the method extends beyond the study of vibrational properties. Linear response provides an analytical way of computing the second derivative of the total energy with respect to a given perturbation. Depending on the nature of this perturbation, a number of properties can be calculated. A perturbation in ionic positions gives the dynamical matrix and phonons; in magnetic field - NMR response; in unit cell vectors - elastic constants; in an electric field - dielectric response, and so on.
The force constants matrix can be obtained by differentiating the Hellmann-Feynman forces on atoms, with respect to ionic coordinates. This procedure reveals that the force constants matrix depends on the ground state electron charge density and on its linear response to a distortion of atomic positions. Due to the variational principle of the density functional formalism, the second order change in energy depends on the first order change in the electron density.
The DFPT formalism is, in many ways, very similar to the density functional theory (DFT) itself. DFT states that the total energy is the functional of the electron density; thus one can solve the DFT equations by minimizing the total energy. Similarly, the DFPT problem can be solved by minimizing the second order perturbation in the total energy, which gives the first order changes in density, wavefunctions and potential (Gonze et al. 1994, Gonze 1997).
This variational technique for solving DFPT problems is a more robust and accurate method than the original Green's function, iterative scheme suggested by Baroni et al. 1987. Both methods should converge to the same solution but the Green's function method does not rely on the variational principle and its convergence properties are thus inferior. Moreover, once the first order change in wavefunctions, ψ(1), is evaluated, then the Green's function scheme evaluates the second order energy, which is not stationary with respect to first-order errors in ψ(1). Thus, the variational scheme of Gonze 1997 is expected to be more accurate.
The electronic second order energy, which is minimized in this approach, as implemented in CASTEP, is:
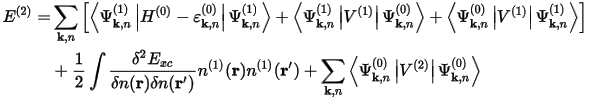
where the superscripts refer to the ground state (0) and first (1) and second (2) order changes, respectively. Similar terms have to be evaluated for the ionic terms in the total energy. The preconditioned conjugate gradients minimization scheme can be used to find the minimum of this functional with respect to the first order wavefunctions. The dynamical matrix for a given q is then evaluated from the converged first order wavefunctions and densities (Gonze 1997).