



Next: 4.2 Partial occupation of
Up: 4. Density-Matrix Formulation
Previous: 4. Density-Matrix Formulation
Contents
In section 2.1 we laid down the fundamental principles of
quantum mechanics in terms of wave-functions and operators. In practice,
however,
we often do not know the precise quantum-mechanical state of the system, but
have some statistical knowledge about the probabilities for the system being
in one of a set of states (note that these probabilities are completely distinct
from the probabilities which arise when a measurement is made). For a fuller
discussion of what follows, see [130].
Suppose that there is a set of orthonormal states
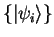 for our system, and that the probabilities that the
system is in each of these states are
for our system, and that the probabilities that the
system is in each of these states are 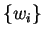 . The expectation
value of an observable
. The expectation
value of an observable 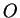 is
is
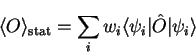 |
(4.1) |
which is a quantum and statistical average.
We define the density-operator as
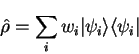 |
(4.2) |
and introduce a complete set of basis states
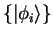 , writing
the
, writing
the
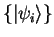 as linear combinations:
as linear combinations:
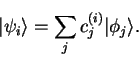 |
(4.3) |
Expressed in terms of this basis, the expectation value becomes
in which the density-matrix 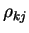 , the matrix representation of the
density-operator in this basis, is defined by
, the matrix representation of the
density-operator in this basis, is defined by
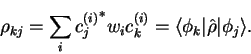 |
(4.5) |
The fact that the probabilities must sum to unity is expressed by the
fact that the trace of the density-matrix is also unity i.e.
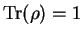 .
A state of the system which corresponds to a single state-vector (i.e. when
.
A state of the system which corresponds to a single state-vector (i.e. when
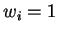 and
and
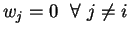 ) is known as a pure state
and for such a state the density-matrix obeys a condition known as
idempotency i.e.
) is known as a pure state
and for such a state the density-matrix obeys a condition known as
idempotency i.e. 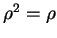 which is only obeyed by matrices
whose eigenvalues are all zero or unity. The more general state introduced
above is known as a mixed state and does not obey the idempotency
condition. Other properties of the density-matrix are that it is Hermitian,
and that in all representations the diagonal elements are always real and
lie in the interval
which is only obeyed by matrices
whose eigenvalues are all zero or unity. The more general state introduced
above is known as a mixed state and does not obey the idempotency
condition. Other properties of the density-matrix are that it is Hermitian,
and that in all representations the diagonal elements are always real and
lie in the interval ![$[0,1]$](img395.gif) .
.




Next: 4.2 Partial occupation of
Up: 4. Density-Matrix Formulation
Previous: 4. Density-Matrix Formulation
Contents
Peter Haynes
![]() for our system, and that the probabilities that the
system is in each of these states are
for our system, and that the probabilities that the
system is in each of these states are ![]() . The expectation
value of an observable
. The expectation
value of an observable ![]() is
is
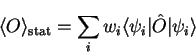
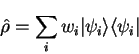
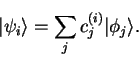
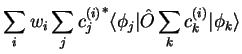
![$\displaystyle \sum_j \sum_k \left[ \sum_i {c_j^{(i)}}^{\ast} w_i c_k^{(i)} \right]
\langle \phi_j \vert {\hat O} \vert \phi_k \rangle$](img387.gif)
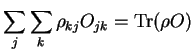
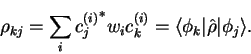
![]() .
A state of the system which corresponds to a single state-vector (i.e. when
.
A state of the system which corresponds to a single state-vector (i.e. when
![]() and
and
![]() ) is known as a pure state
and for such a state the density-matrix obeys a condition known as
idempotency i.e.
) is known as a pure state
and for such a state the density-matrix obeys a condition known as
idempotency i.e. ![]() which is only obeyed by matrices
whose eigenvalues are all zero or unity. The more general state introduced
above is known as a mixed state and does not obey the idempotency
condition. Other properties of the density-matrix are that it is Hermitian,
and that in all representations the diagonal elements are always real and
lie in the interval
which is only obeyed by matrices
whose eigenvalues are all zero or unity. The more general state introduced
above is known as a mixed state and does not obey the idempotency
condition. Other properties of the density-matrix are that it is Hermitian,
and that in all representations the diagonal elements are always real and
lie in the interval ![]() .
.