The importance of the trial/guiding wavefunction in determining the
accuracy of VMC calculations is illustrated by recent work
[33] to calculate the total energy of solid germanium in the
diamond structure using a 2x2x2 supercell containing 16 Ge atoms and
64 valence electrons within both the VMC and DMC formalisms. The
results are illustrated in Figure
.
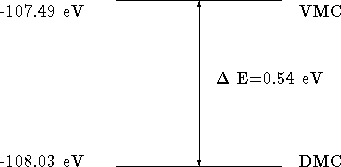
Figure: Difference in the energy of VMC and DMC results for 2x2x2 bulk
germanium in the diamond structure.
The VMC energy and DMC energy are defined as
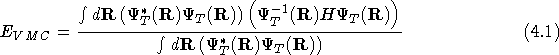
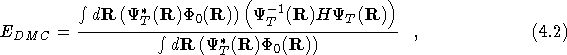
where 
is the wavefunction that 
propagates to during the
diffusion process.
It has already been stressed in section that the DMC
energy is in principle exact (apart from the fixed-node
approximation), i.e. for a given trial/guiding wavefunction , the
DMC energy is equivalent to the lowest variational energy for all
wavefunctions with the same nodal surface as . As the DMC and VMC
[50] calculations share the same trial wavefunction,
and hence have the same nodal surface, the difference in energy
is due only to the difference between the VMC
trial wavefunction and the wavefunction, , to which the
DMC calculation converges to in the long time approximation.
This energy difference acts as a measure of the quality of
, where the quality describes how closely matches the converged
DMC ground state wavefunction, , throughout all of
configuration space. If one is able to optimise the trial/guiding
wavefunction and therefore improve its quality, then the difference
will be reduced and the accuracy of the VMC
calculations is improved.
It is not only the value of the total energy which reflects the quality of a trial/guiding wavefunction. The intrinsic variance of the energy estimator, as defined by
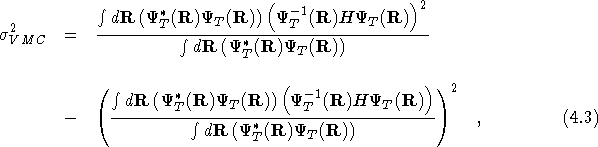
is also important. If one is able to reduce the intrinsic variance,
, of the VMC energy by improving the quality of ,
then the number of VMC moves required to achieve a specific variance
of the mean, 
, decreases linearly with the variance. i.e.
, where N is the number of moves.