Nonlinear core correction
The nonlinear core correction (NLCC) was first proposed by Louie et al. (1982) as a way of obtaining accurate pseudopotential descriptions of magnetic systems. It has been shown, however, that NLCC is equally important for spin non-polarized systems with semicore electrons.
The reason that the NLCC is required is found in the total energy expression in DFT:
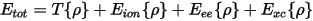
In the pseudopotential formalism, the charge density is divided into core and valence contributions. The energy of the core is assumed to be constant and is subtracted out. Thus, in Eq. CASTEP 19 above the total charge density is replaced by a (pseudo) valence charge density and Eion is evaluated using pseudopotentials.
As a result all interaction between core and valence electrons is transferred to the pseudopotential. This implies linearization with respect to charge density which can only be an approximation to the kinetic energy and the explicitly nonlinear exchange-correlation energy.
This linearization is obviously a good approximation when core and valence densities are well separated in space. However, if there is significant overlap between the two densities, it will be the source of systematic errors and will lead to reduced transferability of the potential.
The solution to the NLCC problem lies in a modifying the pseudopotential generation procedure and the solid-state algorithm. In a typical generation scheme a screened atomic potential Vl is produced for each angular momentum channel subject to certain constraints, for example norm-conservation, matching eigenvalues to all-electron values, and so on.
These screened potentials give rise to atomic pseudowavefunctions that represent valence states only. The valence pseudo charge density is constructed from these wavefunctions and is used to descreen the potential to produce the bare ionic potential:
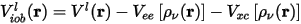
Since the exchange-correlation potential is a nonlinear function of the charge density, it can be shown that this procedure, especially for spin-polarized systems, creates ionic pseudopotentials that are dependent on the valence configuration. Louie et al. (1982) suggested substituting Eq. CASTEP 20 with the following expression:
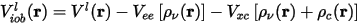
Here the total exchange-correlation potential is subtracted from the screened atomic potential. In addition, the core charge must now be added to the valence charge whenever the exchange-correlation potential is calculated. This additional atomic information has to be passed on to CASTEP and the core charge is deemed to be the same in all applications. A drawback of this is that the core charge is difficult to represent accurately on the Fourier grid used in pseudopotential calculations. Furthermore, the core density is usually bigger than the valence density, so its presence might mask effects related to valence charge density.
The next step in developing the formalism was to introduce the partial core correction. This approach recognizes the fact that only the area of overlap between the core and valence densities is of interest. Core density close to the nucleus is of no consequence although this is precisely the part of the core density that causes the problems described above. Partial NLCC replaces the full core density with a function that coincides with ρc outside a certain radius, and falls off smoothly toward the nucleus.
CASTEP uses a partial core correction with numerical core density in the case of ultrasoft pseudopotentials for certain elements. The database of norm-conserving potentials does not, however, include NLCC information.