Norm-Conserving Pseudopotentials

The main requirement of the pseudopotential approach is that it reproduces the valence charge density associated with chemical bonds. For pseudo and all-electron wavefunctions to be identical beyond the core radius, R_c, the integrals of squared amplitudes of the two functions must be the same (Hamann et al., 1979). This is equivalent to requiring norm-conservation from pseudo wavefunctions, that is, each should carry exactly one electron. This condition ensures correct reproduction of the scattering properties of the pseudopotential.

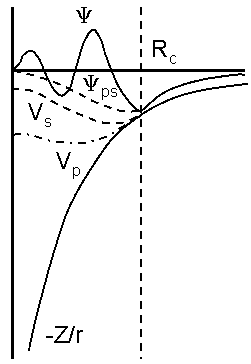
Figure 1. Schematic representation of the all-electron and pseudized wavefunctions and potentials

The typical method for generating pseudopotentials is as follows:

• All-electron calculations are carried out for an isolated atom in a chosen electronic configuration (not necessarily in the ground state). This provides valence electron eigenvalues and valence electron wavefunctions for the atom (shown as ψ in Figure 1).

• Selection of a parameterized form for the ionic pseudopotential (or the pseudo wavefunction).

• The parameters are then adjusted, so that a pseudoatom calculation with the same exchange-correlation potential as in the all-electron atom gives:

  • Pseudowavefunctions, ψ_ps (Figure 1), that match the valence wavefunctions outside some cutoff radius, R_c.

  • Pseudoeigenvalues that are equal to the valence eigenvalues.

This procedure involves direct inversion of the radial Kohn-Sham equation for parameterization of the pseudowavefunctions rather than the pseudopotential. Normalizing each wavefunction, pseudo and all-electron, to one, results in automatically satisfaction of the norm-conservation constraint because of matching the wavefunctions outside R_c.

The ionic pseudopotentials construction uses R_c ranging from one to two times the value of the physical core radius. The smaller the value of R_c, the harder and more transferable the potential. The conflicting effect of R_c creates an obvious trade-off between accuracy and efficiency.

Optimized Pseudopotentials

A number of recipes exist for producing pseudopotentials that are optimized with respect to the energy cutoff required in solid-state calculations.

Lin et al. (1993) suggested the following generation scheme based on the earlier work of Rappé et al. (1990).

1. The pseudo wavefunction ψ_l(r) inside a cutoff radius is expressed as:

   Eq. CASTEP 5

   

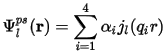
   Where:

   

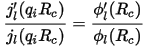
   j_l(q_ir) are spherical Bessel functions with (i-1) zeros between r=0 and r=R_c. The cutoff radius value is as large as possible, consistent with satisfactory transferability of the potential.

2. Minimization of the kinetic energy beyond the cutoff vector q_c determines the coefficients α_i:

   Eq. CASTEP 6

   

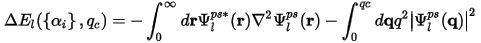
   where q_c is chosen to be equal to q₄ from Eq. CASTEP 5. Lagrange multipliers satisfy some additional constraints:

   • The normalization of the pseudowavefunction.
   • The continuity of the first two derivatives of the pseudowavefunction at R_c.
3. The standard step of inverting the radial Kohn-Sham equation produces a smooth pseudopotential with optimal convergence properties.

Lee (1996) suggested further enhancements and it is essentially this scheme that generated the bulk of norm-conserving pseudopotentials in the CASTEP database. This generation method eliminates the condition that the second derivative of the pseudo wavefunction must be continuous at a given cutoff radius because it automatically satisfies the second derivative constraint. The scheme allows you to tune q_c for a given R_c to optimize the accuracy and efficiency of a pseudopotential.

The USP implementation allows you to run CASTEP calculations with a lower energy cutoff than their NCP counterparts; producing a clear advantage in terms of the calculation time. However, USP formalism is more complex and becomes close to intractable for such complex concepts as linear response implementation for phonons or NMR properties, or for nonlocal exchange-correlation functionals. There is a number of tasks and properties that CASTEP can address only with norm-conserving potentials. The database of tabulated NCPs available in Materials Studio is rather old and in some cases might contain potentials that have not been tested sufficiently. A recommended alternative is to use on-the-fly generated norm-conserving pseudopotentials that are more accurate and much better tested.