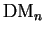Next: General outline of the
Up: Normalisation constraint
Previous: Density-kernel variation
Contents
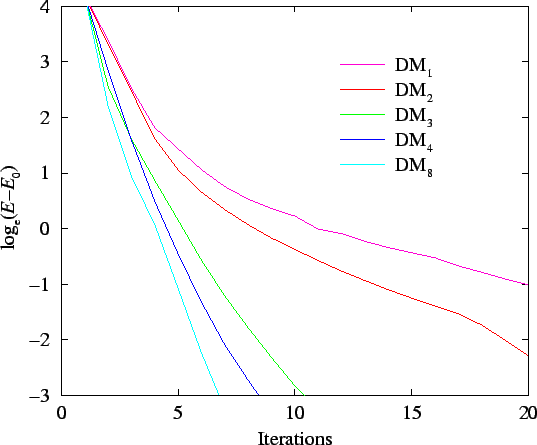
The electron number gradient with respect to the support functions
is given in section 7.3 and denoted by
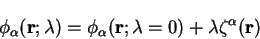 :
:
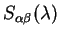 |
(7.82) |
The support function variation is again parameterised by the parameter
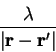 :
:
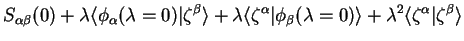 |
(7.83) |
and this results in the following quadratic variation of the overlap matrix
which defines the matrices 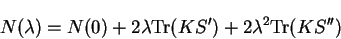 and
and 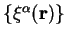 . The variation of the electron
number is therefore also quadratic
. The variation of the electron
number is therefore also quadratic
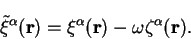 |
(7.85) |
and the roots of this expression can be found to correct the electron number.
We consider a general search direction for the localised functions denoted
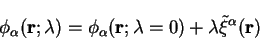 and modify this search direction to obtain the
direction which maintains the electron number to first order:
and modify this search direction to obtain the
direction which maintains the electron number to first order:
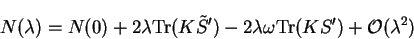 |
(7.86) |
Now varying the localised functions according to
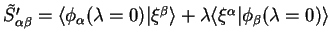 |
(7.87) |
results in the following variation of the electron number:
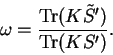 |
(7.88) |
where
 .
Thus to maintain the electron number to first order, we choose
.
Thus to maintain the electron number to first order, we choose
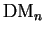 |
(7.89) |
In this case, the electron number is not constant along the search direction,
but will still vary quadratically, so that it is necessary to correct the
density-matrix before evaluating the total functional.




Next: General outline of the
Up: Normalisation constraint
Previous: Density-kernel variation
Contents
Peter D. Haynes
1999-09-21
![]() :
:
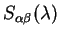
![]() and modify this search direction to obtain the
direction which maintains the electron number to first order:
and modify this search direction to obtain the
direction which maintains the electron number to first order: