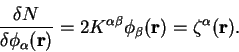Next: Support function variation
Up: Normalisation constraint
Previous: Normalisation constraint
Contents
In section 7.3 the electron number gradient with respect to
the density-kernel, which is here denoted 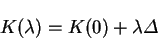 , is given as
, is given as
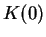 |
(7.75) |
The density-kernel along this search direction 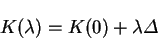 is
parameterised by
is
parameterised by 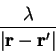 as
as
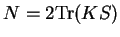 |
(7.76) |
where 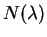 denotes the initial density-matrix.
The electron number, given by
denotes the initial density-matrix.
The electron number, given by
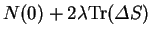 thus behaves linearly:
thus behaves linearly:
and it is a trivial matter to calculate the required value of 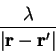 to return the electron number to its correct value.
to return the electron number to its correct value.
In general during the minimisation, the search direction is
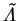 , and again this search can be parameterised by a single
parameter
, and again this search can be parameterised by a single
parameter 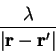 :
:
 |
(7.78) |
We wish to project out from 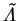 that component which is
parallel to
that component which is
parallel to 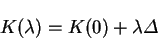 . The modified search direction
. The modified search direction
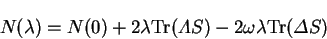 can be written as
can be written as
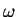 |
(7.79) |
The variation of the electron number along this modified direction is
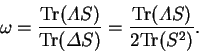 |
(7.80) |
and we wish the coefficient of the linear term in 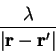 to vanish,
which defines the required value of
to vanish,
which defines the required value of 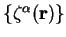 to be
to be
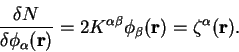 |
(7.81) |
Since the electron number depends linearly upon the density-kernel,
after this projection, the electron number is constant along the modified
search direction, and the electron number need not be corrected after
a trial step is taken.




Next: Support function variation
Up: Normalisation constraint
Previous: Normalisation constraint
Contents
Peter D. Haynes
1999-09-21
![]() , is given as
, is given as
![]() , and again this search can be parameterised by a single
parameter
, and again this search can be parameterised by a single
parameter ![]() :
: