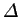Next: Normalisation constraint
Up: Practical details
Previous: Practical details
Contents
The support functions are expanded in spherical-wave basis functions:
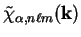 |
(7.71) |
For a functional of the support functions
![$f[\{ \phi_{\alpha} \}]$](img1077.gif) , the
derivative with respect to the expansion coefficients is
, the
derivative with respect to the expansion coefficients is
For example, for the derivative of the total energy,
![\begin{displaymath}
\frac{\delta E[\rho]}{\delta \phi_{\alpha}({\bf r})} =
4 K^{\alpha \beta} {\hat H} \phi_{\beta}({\bf r}) ,
\end{displaymath}](img1082.gif) |
(7.73) |
we obtain
in which
 denotes the matrix element of the Kohn-Sham
Hamiltonian with respect to the spherical-wave basis functions.
denotes the matrix element of the Kohn-Sham
Hamiltonian with respect to the spherical-wave basis functions.




Next: Normalisation constraint
Up: Practical details
Previous: Practical details
Contents
Peter D. Haynes
1999-09-21
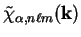
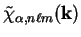
![$\displaystyle \frac{\partial f[\{ \phi_{\alpha} \}]}{\partial c^{n \ell m}_{(\beta)}}$](img1078.gif)
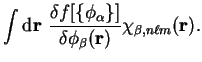
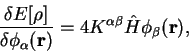
![$\displaystyle \int {\mathrm d}{\bf r}~\frac{\delta f[ \{ \phi_{\alpha} \} ]}
{\delta \phi_{\beta}({\bf r})}
\chi_{\beta , n \ell m}({\bf r}) .$](img1081.gif)
![\begin{displaymath}
\frac{\delta E[\rho]}{\delta \phi_{\alpha}({\bf r})} =
4 K^{\alpha \beta} {\hat H} \phi_{\beta}({\bf r}) ,
\end{displaymath}](img1082.gif)
![$\displaystyle \frac{\partial E[\rho]}{\partial c^{n \ell m}_{(\beta)}}$](img1083.gif)