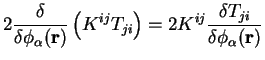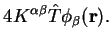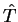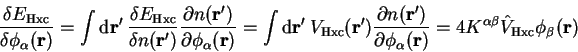Next: Hartree and exchange-correlation energies
Up: Support function derivatives
Previous: Support function derivatives
Contents
We define the kinetic energy operator
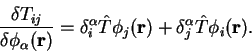 , whose matrix elements are
, whose matrix elements are
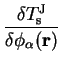 |
(7.30) |
Since the operator is Hermitian,
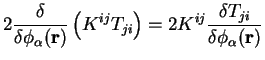 |
(7.31) |
Therefore
The derivation for the pseudopotential energy is identical with the
replacement of 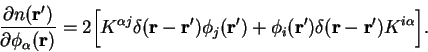 by the pseudopotential operator, and so the result
for the sum of these energies is just
by the pseudopotential operator, and so the result
for the sum of these energies is just
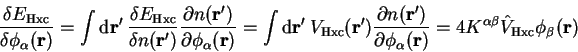 |
(7.33) |
Peter D. Haynes
1999-09-21
![]() , whose matrix elements are
, whose matrix elements are