



Next: Computational implementation
Up: Corrected penalty functional method
Previous: Further examples of penalty
Contents
Minimisation efficiency
In this section we discuss the efficiency of the conjugate gradients
algorithm to minimise the total functional. We restrict the discussion
to the penalty functional introduced in section 6.2.1.
The total functional derived from this penalty functional appears to
possess multiple
local minima since the penalty functional itself is minimal for all
idempotent density-matrices. However, most of these local minima do not
correspond to density-matrices obeying the correct normalisation
constraint and are therefore eliminated by imposing this constraint
during the minimisation, as will be shown in chapter 7.
Of the remaining minima, only one corresponds to the situation in which
the lowest bands are occupied, and when the support functions are also
varied, all other minima become unstable with respect to this one
(i.e. these are minima with respect to occupation number variations but
not orbital variations).
Numerical investigations into this
matter have been carried out and no problems arising from multiple minima
have been observed (the minimised total functional has the same value
independent of the starting point).
The efficiency with which the conjugate gradients scheme is able to
minimise a function is known to depend upon the condition number
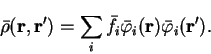 , the ratio of the largest curvature to the smallest curvature
at the minimum. The condition number may be calculated exactly by
determining the Hessian matrix at the minimum, but may also be estimated
as follows [153].
, the ratio of the largest curvature to the smallest curvature
at the minimum. The condition number may be calculated exactly by
determining the Hessian matrix at the minimum, but may also be estimated
as follows [153].
Consider the minimising density-matrix 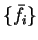 expanded in terms of a
set of orthonormal orbitals
expanded in terms of a
set of orthonormal orbitals
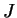 :
:
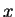 |
(6.30) |
Consider first perturbing the occupation numbers subject to the normalisation
constraint i.e. increasing the occupation of some orbital labelled 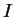 by
by 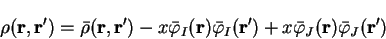 at the
expense of another orbital labelled
at the
expense of another orbital labelled 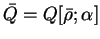 . The density-matrix becomes
. The density-matrix becomes
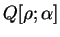 |
(6.31) |
Defining
![${\bar Q} = Q[{\bar \rho};\alpha]$](img893.gif) and using the orthonormality of the
orbitals,
and using the orthonormality of the
orbitals,
and the curvature at the minimum is
![\begin{displaymath}
\left. \frac{\partial^2 Q[{\rho};\alpha]}{\partial x^2}\righ...
...f}_I (1 - {\bar f}_I) - 3{\bar f}_J (1 - {\bar f}_J) \right] .
\end{displaymath}](img898.gif) |
(6.33) |
Assuming that 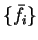 is approximately idempotent so that
both
is approximately idempotent so that
both 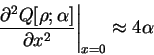 and
and 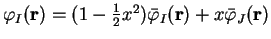 are either roughly zero or unity,
are either roughly zero or unity,
![\begin{displaymath}
\left. \frac{\partial^2 Q[{\rho};\alpha]}{\partial x^2}\right\vert _{x=0}
\approx 4 \alpha
\end{displaymath}](img901.gif) |
(6.34) |
i.e. to first order, the curvature is independent of the choice of orbitals
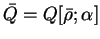 and
and 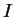 so that the functional is spherical when this type of variation
is considered, and the condition number is approximately unity.
so that the functional is spherical when this type of variation
is considered, and the condition number is approximately unity.
The second type of variation is a unitary transformation of the orbitals
i.e.
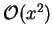 and
and
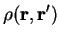 , which maintains normalisation of the
density-matrix to
, which maintains normalisation of the
density-matrix to 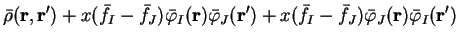 .
In this case
.
In this case
and similarly
![\begin{displaymath}
Q[{\rho};\alpha] = {\bar Q} + x^2 ({\bar f}_I - {\bar f}_J)({\bar
\varepsilon}_J - {\bar \varepsilon}_I) + {\cal O}(x^3)
\end{displaymath}](img909.gif) |
(6.36) |
so that
![\begin{displaymath}
\left. \frac{\partial^2 Q[{\rho};\alpha]}{\partial x^2}\righ...
...I - {\bar f}_J)({\bar \varepsilon}_J - {\bar \varepsilon}_I) .
\end{displaymath}](img910.gif) |
(6.37) |
The maximum curvature is thus obtained when
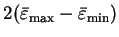 and
and
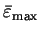 and equals
and equals
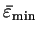 where
where
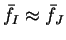 and
and
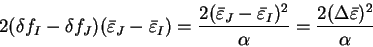 are the maximum and minimum energy
eigenvalues of the orbitals
are the maximum and minimum energy
eigenvalues of the orbitals
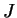 .
The minimum curvature is obtained when
.
The minimum curvature is obtained when
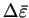 and
is therefore
and
is therefore
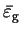 |
(6.38) |
where
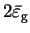 is the minimum energy eigenvalue spacing.
This curvature corresponds to unitary changes confined within the
occupied or unoccupied subspaces with no mixing between, and the energy is
indeed invariant under such changes. However, choosing to work with
localised functions essentially defines a particular unitary transformation
for the wave-functions, so that these variations are generally eliminated.
If this is the case, then the minimum curvature will then
be obtained in the same way as the maximum curvature, but seeking the
minimum difference in energy eigenvalues between valence and conduction
bands, which is the band gap
is the minimum energy eigenvalue spacing.
This curvature corresponds to unitary changes confined within the
occupied or unoccupied subspaces with no mixing between, and the energy is
indeed invariant under such changes. However, choosing to work with
localised functions essentially defines a particular unitary transformation
for the wave-functions, so that these variations are generally eliminated.
If this is the case, then the minimum curvature will then
be obtained in the same way as the maximum curvature, but seeking the
minimum difference in energy eigenvalues between valence and conduction
bands, which is the band gap
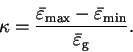 . The
minimum curvature is thus
. The
minimum curvature is thus
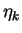 and the
condition number is given by
and the
condition number is given by
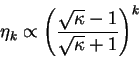 |
(6.39) |
This is an encouraging result, since the condition number is independent
of the system-size.
The length of the error vector after 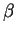 iterations,
iterations,
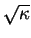 is related to
is related to 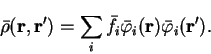 by [154]
by [154]
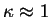 |
(6.40) |
and the number of iterations required to converge to a given precision is
therefore proportional to 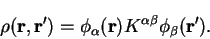 in the limit of large
in the limit of large 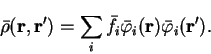 ,
and so independent of system-size.
,
and so independent of system-size.
Reviewing the results for both types of variation, we note that the
minimisation with respect to occupation numbers (the first type) is very
efficient, since
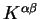 , whereas the minimisation with respect to
orbitals is less efficient, depending upon the ratio of the total width of
the eigenvalue spectrum to the band gap.
Preconditioning schemes to compress the eigenvalue spectrum have been
developed for use with plane-waves [81] and also with
, whereas the minimisation with respect to
orbitals is less efficient, depending upon the ratio of the total width of
the eigenvalue spectrum to the band gap.
Preconditioning schemes to compress the eigenvalue spectrum have been
developed for use with plane-waves [81] and also with
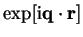 -splines [155], and a similar scheme for the spherical-wave
basis functions would also improve the rate of convergence.
Nevertheless, we do not expect a significant change in the
number of conjugate gradient steps required to converge to the minimum as the
system-size increases.
In practical implementations, discussed in chapter 7, these
two types of variation are not strictly separated, both the occupation numbers and the
orbitals being varied simultaneously, so that these results are hard to
confirm numerically, although no significant increase in the number of
iterations required to converge to a given accuracy is observed as the
system-size increases.
-splines [155], and a similar scheme for the spherical-wave
basis functions would also improve the rate of convergence.
Nevertheless, we do not expect a significant change in the
number of conjugate gradient steps required to converge to the minimum as the
system-size increases.
In practical implementations, discussed in chapter 7, these
two types of variation are not strictly separated, both the occupation numbers and the
orbitals being varied simultaneously, so that these results are hard to
confirm numerically, although no significant increase in the number of
iterations required to converge to a given accuracy is observed as the
system-size increases.




Next: Computational implementation
Up: Corrected penalty functional method
Previous: Further examples of penalty
Contents
Peter D. Haynes
1999-09-21
![]() , the ratio of the largest curvature to the smallest curvature
at the minimum. The condition number may be calculated exactly by
determining the Hessian matrix at the minimum, but may also be estimated
as follows [153].
, the ratio of the largest curvature to the smallest curvature
at the minimum. The condition number may be calculated exactly by
determining the Hessian matrix at the minimum, but may also be estimated
as follows [153].
![]() expanded in terms of a
set of orthonormal orbitals
expanded in terms of a
set of orthonormal orbitals
![]() :
:
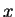
![\begin{displaymath}
\left. \frac{\partial^2 Q[{\rho};\alpha]}{\partial x^2}\righ...
...f}_I (1 - {\bar f}_I) - 3{\bar f}_J (1 - {\bar f}_J) \right] .
\end{displaymath}](img898.gif)
![\begin{displaymath}
\left. \frac{\partial^2 Q[{\rho};\alpha]}{\partial x^2}\right\vert _{x=0}
\approx 4 \alpha
\end{displaymath}](img901.gif)
![]() and
and
![]() , which maintains normalisation of the
density-matrix to
, which maintains normalisation of the
density-matrix to ![]() .
In this case
.
In this case
![\begin{displaymath}
\left. \frac{\partial^2 Q[{\rho};\alpha]}{\partial x^2}\righ...
...I - {\bar f}_J)({\bar \varepsilon}_J - {\bar \varepsilon}_I) .
\end{displaymath}](img910.gif)
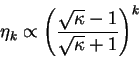
![]() iterations,
iterations,
![]() is related to
is related to ![]() by [154]
by [154]
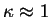
![]() , whereas the minimisation with respect to
orbitals is less efficient, depending upon the ratio of the total width of
the eigenvalue spectrum to the band gap.
Preconditioning schemes to compress the eigenvalue spectrum have been
developed for use with plane-waves [81] and also with
, whereas the minimisation with respect to
orbitals is less efficient, depending upon the ratio of the total width of
the eigenvalue spectrum to the band gap.
Preconditioning schemes to compress the eigenvalue spectrum have been
developed for use with plane-waves [81] and also with
![]() -splines [155], and a similar scheme for the spherical-wave
basis functions would also improve the rate of convergence.
Nevertheless, we do not expect a significant change in the
number of conjugate gradient steps required to converge to the minimum as the
system-size increases.
In practical implementations, discussed in chapter 7, these
two types of variation are not strictly separated, both the occupation numbers and the
orbitals being varied simultaneously, so that these results are hard to
confirm numerically, although no significant increase in the number of
iterations required to converge to a given accuracy is observed as the
system-size increases.
-splines [155], and a similar scheme for the spherical-wave
basis functions would also improve the rate of convergence.
Nevertheless, we do not expect a significant change in the
number of conjugate gradient steps required to converge to the minimum as the
system-size increases.
In practical implementations, discussed in chapter 7, these
two types of variation are not strictly separated, both the occupation numbers and the
orbitals being varied simultaneously, so that these results are hard to
confirm numerically, although no significant increase in the number of
iterations required to converge to a given accuracy is observed as the
system-size increases.