



Next: Further examples of penalty
Up: Corrected penalty functional method
Previous: Corrected penalty functional method
Contents
Derivation of the correction
In this section we present a new method to perform total energy calculations
using a penalty functional to enforce idempotency approximately.
We define a generalised energy functional
![$Q[{\rho};\alpha]$](img842.gif) for trial
density-matrices
for trial
density-matrices 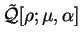 by
by
![\begin{displaymath}
Q[{\rho};\alpha] = E[\rho] + \alpha P[\rho] .
\end{displaymath}](img843.gif) |
(6.15) |
![$P[\rho]$](img844.gif) represents the penalty functional, which in this new
method is required to be analytic at all points
so that efficient minimisation schemes such as conjugate gradients may be
applied. The simplest example is to take the square of Kohn's penalty
functional i.e.
represents the penalty functional, which in this new
method is required to be analytic at all points
so that efficient minimisation schemes such as conjugate gradients may be
applied. The simplest example is to take the square of Kohn's penalty
functional i.e.
![\begin{displaymath}
P[{\rho}] = \int {\mathrm d}{\bf r}~\left[ {\rho}^2
\left( 1...
...ht]({\bf r},{\bf r}) =
\sum_i f_i^2 \left( 1 - f_i \right)^2 ,
\end{displaymath}](img845.gif) |
(6.16) |
but other choices are also possible (section 6.2.2).
This penalty functional is sketched in figure 6.5.
Figure 6.5:
One possible choice of analytic penalty functional.
|
Since the penalty functional becomes large as the density-matrix becomes
less idempotent, minimisation of the total functional
![$Q[{\rho};\alpha]$](img842.gif) is stable against run-away solutions in which
is stable against run-away solutions in which
 for occupied bands and
for occupied bands and
 for unoccupied
bands. However, as illustrated in the sketch in figure 6.6,
the minimising density-matrix is only approximately idempotent. In this
particular case of an unoccupied band, the total functional is minimised
when this band is negatively occupied i.e. for
for unoccupied
bands. However, as illustrated in the sketch in figure 6.6,
the minimising density-matrix is only approximately idempotent. In this
particular case of an unoccupied band, the total functional is minimised
when this band is negatively occupied i.e. for 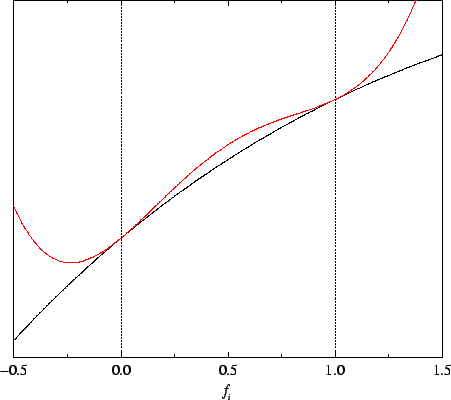 .
In general the minimising density-matrix
.
In general the minimising density-matrix 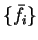 will have eigenvalues
lying
outside the interval
will have eigenvalues
lying
outside the interval ![$[0,1]$](img396.gif) , so that the energy calculated from such a
density-matrix will be below the true ground-state energy.
, so that the energy calculated from such a
density-matrix will be below the true ground-state energy.
Figure 6.6:
Schematic illustration of the analytic penalty functional: behaviour of the total energy (black)
and total functional (red) with respect to a single occupation number for an
unoccupied band.
|
We denote the set of occupation numbers which minimise the total functional
![$Q[{\rho};\alpha]$](img842.gif) by
by
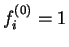 and the errors in these
occupation numbers with respect to idempotency by
and the errors in these
occupation numbers with respect to idempotency by
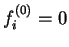 where
where 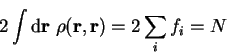 for occupied bands and
for occupied bands and 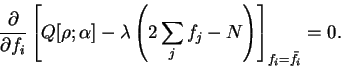 for unoccupied bands.
Since
for unoccupied bands.
Since
![$Q[{\rho};\alpha]$](img842.gif) is minimised by
is minimised by 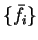 , it is a
minimum with respect to all changes in the occupation numbers which maintain
the normalisation constraint
, it is a
minimum with respect to all changes in the occupation numbers which maintain
the normalisation constraint
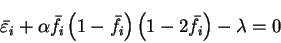 |
(6.17) |
which is imposed by introducing a Lagrange multiplier 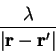 :
:
![\begin{displaymath}
\frac{\partial}{\partial f_i} \left[
Q[{\rho};\alpha] - \lam...
...eft( 2 \sum_j f_j - N \right)
\right]_{f_i = {\bar f}_i} = 0 .
\end{displaymath}](img855.gif) |
(6.18) |
Using Janak's theorem for the derivative of the energy functional we obtain
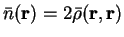 |
(6.19) |
in which
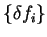 are the eigenvalues of the Hamiltonian
obtained from the electronic density
are the eigenvalues of the Hamiltonian
obtained from the electronic density
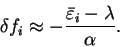 and are therefore different from the true ground-state
eigenvalues.
Assuming
and are therefore different from the true ground-state
eigenvalues.
Assuming  to be sufficiently large so that the errors
to be sufficiently large so that the errors
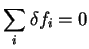 are small,
are small,
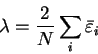 |
(6.20) |
Application of the normalisation constraint 6.17 requires
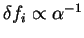 from which we obtain the value of
the Lagrange multiplier
from which we obtain the value of
the Lagrange multiplier 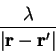 :
:
 |
(6.21) |
which is the mean energy eigenvalue. The variance of the
errors in the occupation numbers is thus related to the variance of the
energy eigenvalues, scaled by the parameter  . Therefore, as is
intuitively expected, the errors in the occupation numbers decrease as
. Therefore, as is
intuitively expected, the errors in the occupation numbers decrease as
 is increased. More precisely,
is increased. More precisely,
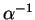 and
this behaviour is confirmed numerically in figure 6.7.
and
this behaviour is confirmed numerically in figure 6.7.
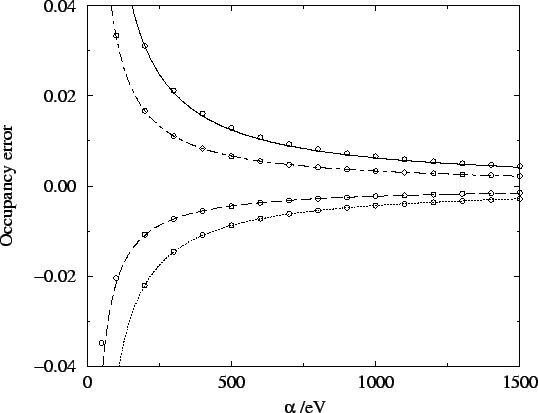
Figure 6.7:
Variation of the occupation number errors with  . Lines
show the best fit to
. Lines
show the best fit to 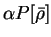 behaviour.
behaviour.
|
For small deviations from idempotency, the penalty functional
![$\displaystyle{P[{\bar \rho}] \approx \sum_i \delta f_i^2}$](img866.gif) so that the
penalty contribution to the minimised total functional,
so that the
penalty contribution to the minimised total functional,
![$\alpha P[{\bar \rho}]$](img867.gif) also decreases in proportion to
also decreases in proportion to 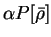 . Hence the energy approaches the
true ground-state energy as
. Hence the energy approaches the
true ground-state energy as
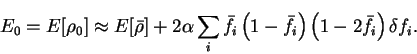 , again with an
error which decreases as
, again with an
error which decreases as 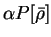 . This
. This 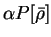 convergence
is unsatisfactory for practical applications, since it requires large
values of
convergence
is unsatisfactory for practical applications, since it requires large
values of  to obtain accurate estimates of the ground-state energy,
and for large values of
to obtain accurate estimates of the ground-state energy,
and for large values of  the penalty term dominates the total
functional and hinders efficient minimisation of the energy term.
We now proceed to derive a correction to the estimated energy which allows
accurate values for the ground-state energy to be obtained from the
approximately idempotent density-matrices which minimise the total
functional.
the penalty term dominates the total
functional and hinders efficient minimisation of the energy term.
We now proceed to derive a correction to the estimated energy which allows
accurate values for the ground-state energy to be obtained from the
approximately idempotent density-matrices which minimise the total
functional.
At the minimum of the total functional,
![\begin{displaymath}
\left. \frac{\partial Q[{\rho};\alpha]}{\partial f_i} \right...
... \left( 1 - {\bar f}_i \right) \left( 1 - 2 {\bar f}_i \right)
\end{displaymath}](img869.gif) |
(6.22) |
and this expression can be used to construct a first order Taylor
expansion for the total energy with respect to the occupation numbers.
We thus estimate the true ground-state energy 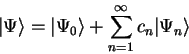 to be
to be
![\begin{displaymath}
E_0 = E[\rho_0] \approx E[{\bar \rho}] + 2 \alpha \sum_i
{\b...
...{\bar f}_i \right) \left( 1 - 2 {\bar f}_i \right)
\delta f_i.
\end{displaymath}](img870.gif) |
(6.23) |
For occupied bands,
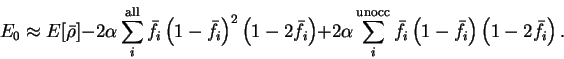 whereas for unoccupied
bands
whereas for unoccupied
bands
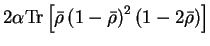 so that
so that
![\begin{displaymath}
E_0 \approx E[{\bar \rho}] - 2 \alpha \sum_i^{\rm all} {\bar...
...left( 1 - {\bar f}_i \right) \left( 1 - 2 {\bar f}_i \right) .
\end{displaymath}](img873.gif) |
(6.24) |
The first term of the correction has been written as a sum over all bands
so that it can be expressed in terms of the trace
![$2 \alpha {\rm Tr} \left[
{\bar \rho} \left( 1 - {\bar \rho} \right)^2 \left( 1 - 2 {\bar \rho} \right)
\right]$](img874.gif) which can always be evaluated in
which can always be evaluated in  operations. The
second term only contributes when unoccupied bands are included in the
calculation, which is not necessary for insulators. Since a single
eigenvalue of the (sparse) density-matrix can always be obtained in
operations. The
second term only contributes when unoccupied bands are included in the
calculation, which is not necessary for insulators. Since a single
eigenvalue of the (sparse) density-matrix can always be obtained in
 operations, it is possible to evaluate the correction for
a small number (
operations, it is possible to evaluate the correction for
a small number ( ) of unoccupied bands and retain the linear-scaling.
However, we note that the correction need only be calculated once the
minimum of the total functional has been found, so that a single
) of unoccupied bands and retain the linear-scaling.
However, we note that the correction need only be calculated once the
minimum of the total functional has been found, so that a single
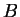 step to obtain all of the occupation numbers will still
be a tiny fraction of the total computational effort.
step to obtain all of the occupation numbers will still
be a tiny fraction of the total computational effort.
The error in a Taylor expansion is generally estimated by considering
the lowest order term omitted, which in this case is
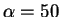 |
(6.25) |
where 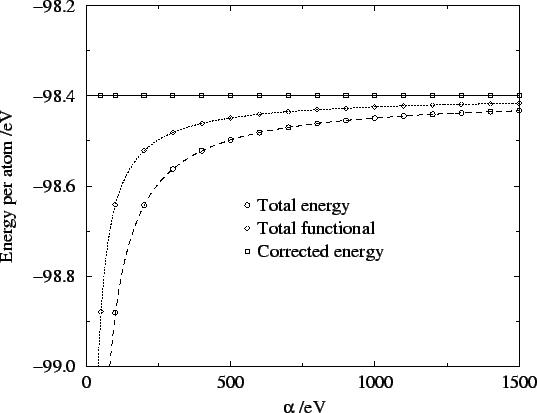 is the chemical hardness matrix. Unfortunately this
matrix is not guaranteed to be either positive or negative definite,
and so the estimate of the ground-state energy 6.24 is not a strict
upper or lower bound to the true energy. As will be seen shortly, this error
is generally much smaller than other sources of error (such as the finite
support region size, with respect to which the energy does behave
variationally) so that this is not an issue in practice.
is the chemical hardness matrix. Unfortunately this
matrix is not guaranteed to be either positive or negative definite,
and so the estimate of the ground-state energy 6.24 is not a strict
upper or lower bound to the true energy. As will be seen shortly, this error
is generally much smaller than other sources of error (such as the finite
support region size, with respect to which the energy does behave
variationally) so that this is not an issue in practice.
In figure 6.8 the energy, total functional and corrected energy
are plotted for different values of the parameter  . These results
confirm the
. These results
confirm the 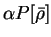 behaviour of the energy and penalty functionals,
and the error in the corrected energy even for
behaviour of the energy and penalty functionals,
and the error in the corrected energy even for 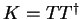 eV is smaller
than
eV is smaller
than 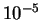 eV per atom. Thus we have achieved our aim of being able
to obtain accurate estimates of the ground-state energy from approximate
density-matrices which minimise the total functional for values of
eV per atom. Thus we have achieved our aim of being able
to obtain accurate estimates of the ground-state energy from approximate
density-matrices which minimise the total functional for values of
 for which efficient minimisation is possible.
for which efficient minimisation is possible.
Figure 6.8:
Total energy, total functional and corrected energy versus  . Lines are best fits to
. Lines are best fits to 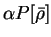 behaviour.
behaviour.
|




Next: Further examples of penalty
Up: Corrected penalty functional method
Previous: Corrected penalty functional method
Contents
Peter D. Haynes
1999-09-21
![]() for trial
density-matrices
for trial
density-matrices ![]() by
by
![\begin{displaymath}
P[{\rho}] = \int {\mathrm d}{\bf r}~\left[ {\rho}^2
\left( 1...
...ht]({\bf r},{\bf r}) =
\sum_i f_i^2 \left( 1 - f_i \right)^2 ,
\end{displaymath}](img845.gif)
![\includegraphics [width=10cm]{mypen.eps}](img849.gif)
![]() by
by
![]() and the errors in these
occupation numbers with respect to idempotency by
and the errors in these
occupation numbers with respect to idempotency by
![]() where
where ![]() for occupied bands and
for occupied bands and ![]() for unoccupied bands.
Since
for unoccupied bands.
Since
![]() is minimised by
is minimised by ![]() , it is a
minimum with respect to all changes in the occupation numbers which maintain
the normalisation constraint
, it is a
minimum with respect to all changes in the occupation numbers which maintain
the normalisation constraint
![\begin{displaymath}
\frac{\partial}{\partial f_i} \left[
Q[{\rho};\alpha] - \lam...
...eft( 2 \sum_j f_j - N \right)
\right]_{f_i = {\bar f}_i} = 0 .
\end{displaymath}](img855.gif)

![]() so that the
penalty contribution to the minimised total functional,
so that the
penalty contribution to the minimised total functional,
![]() also decreases in proportion to
also decreases in proportion to ![]() . Hence the energy approaches the
true ground-state energy as
. Hence the energy approaches the
true ground-state energy as
![]() , again with an
error which decreases as
, again with an
error which decreases as ![]() . This
. This ![]() convergence
is unsatisfactory for practical applications, since it requires large
values of
convergence
is unsatisfactory for practical applications, since it requires large
values of ![]() to obtain accurate estimates of the ground-state energy,
and for large values of
to obtain accurate estimates of the ground-state energy,
and for large values of ![]() the penalty term dominates the total
functional and hinders efficient minimisation of the energy term.
We now proceed to derive a correction to the estimated energy which allows
accurate values for the ground-state energy to be obtained from the
approximately idempotent density-matrices which minimise the total
functional.
the penalty term dominates the total
functional and hinders efficient minimisation of the energy term.
We now proceed to derive a correction to the estimated energy which allows
accurate values for the ground-state energy to be obtained from the
approximately idempotent density-matrices which minimise the total
functional.
![\begin{displaymath}
\left. \frac{\partial Q[{\rho};\alpha]}{\partial f_i} \right...
... \left( 1 - {\bar f}_i \right) \left( 1 - 2 {\bar f}_i \right)
\end{displaymath}](img869.gif)
![\begin{displaymath}
E_0 = E[\rho_0] \approx E[{\bar \rho}] + 2 \alpha \sum_i
{\b...
...{\bar f}_i \right) \left( 1 - 2 {\bar f}_i \right)
\delta f_i.
\end{displaymath}](img870.gif)
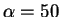
![]() . These results
confirm the
. These results
confirm the ![]() behaviour of the energy and penalty functionals,
and the error in the corrected energy even for
behaviour of the energy and penalty functionals,
and the error in the corrected energy even for ![]() eV is smaller
than
eV is smaller
than ![]() eV per atom. Thus we have achieved our aim of being able
to obtain accurate estimates of the ground-state energy from approximate
density-matrices which minimise the total functional for values of
eV per atom. Thus we have achieved our aim of being able
to obtain accurate estimates of the ground-state energy from approximate
density-matrices which minimise the total functional for values of
![]() for which efficient minimisation is possible.
for which efficient minimisation is possible.
![\includegraphics [width=12cm]{corr.eps}](img879.gif)