The results in equations
5.19, 5.20, 5.22 and
5.23 have been
written in a form which shows that in general each term can be
represented by a real numerical prefactor, integers which are the
powers of
![]() and one further integer
to signify the presence of one of the terms
and one further integer
to signify the presence of one of the terms
![]() . When these terms are combined and differentiated by the
. When these terms are combined and differentiated by the
![]() , the general term also needs integers to represent powers
of
, the general term also needs integers to represent powers
of
![]() . Therefore a general term in the
expressions for
. Therefore a general term in the
expressions for
![]() and
and
![]() could be
represented by a data structure consisting of one real variable
could be
represented by a data structure consisting of one real variable ![]() and ten integer variables
and ten integer variables ![]() as follows:
as follows:
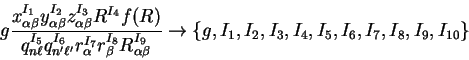 |
(5.45) |
| (5.46) |
The cost of calculating the analytic matrix elements increases dramatically
as higher angular momentum components are included. In general, a much smaller
value of
![]() is used than is ``recommended'' by the kinetic energy
cut-off. However, these basis functions are being used to describe
functions localised in overlapping regions, and in this instance, a
degree of ``under-completeness'' is desirable. If the basis functions formed a
complete set (up to a given kinetic energy cut-off) in each support
region, then a variation which is confined
to the overlapping region can be equally described by variations in either
region. Symmetric and antisymmetric combinations of these variations can
be formed, the antisymmetric variation vanishing and thus leaving the density-matrix invariant. Therefore
this superposition results in directions in the parameter space with very
small curvature which degrade the efficiency of minimisation algorithms
(see section 6.2.3). When working with overlapping
support functions, it is therefore better to treat
is used than is ``recommended'' by the kinetic energy
cut-off. However, these basis functions are being used to describe
functions localised in overlapping regions, and in this instance, a
degree of ``under-completeness'' is desirable. If the basis functions formed a
complete set (up to a given kinetic energy cut-off) in each support
region, then a variation which is confined
to the overlapping region can be equally described by variations in either
region. Symmetric and antisymmetric combinations of these variations can
be formed, the antisymmetric variation vanishing and thus leaving the density-matrix invariant. Therefore
this superposition results in directions in the parameter space with very
small curvature which degrade the efficiency of minimisation algorithms
(see section 6.2.3). When working with overlapping
support functions, it is therefore better to treat
![]() as a convergence parameter along with, rather than derived from,
as a convergence parameter along with, rather than derived from,
![]() .
.