



Next: 3. Quantum Mechanics of
Up: 2. Many-body Quantum Mechanics
Previous: 2.3 Identical particles
Contents
2.4 Variational principles
In section 2.1 we outlined the basic principles of quantum
mechanics, and in particular noted the rôle of the quantity
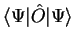 as the expectation value of the observable
corresponding to the operator
as the expectation value of the observable
corresponding to the operator 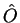 . In that section, mention was briefly
made of the relationship:
. In that section, mention was briefly
made of the relationship:
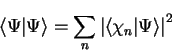 |
(2.41) |
which is simply derived from equations 2.5, 2.6
and 2.8.
If we relax the restriction on orthonormalisation, the expression for the
expectation value becomes
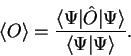 |
(2.42) |
We now consider the expectation value of the Hamiltonian operator for the
electrons, defined in equation 2.19 and reproduced here:
![\begin{displaymath}
{\hat H} \vert \Psi \rangle =
\left[ -\frac{1}{2} \sum_i \n...
...right\vert} \right]
\vert \Psi \rangle = E \vert \Psi \rangle
\end{displaymath}](img140.gif) |
(2.43) |
in which the electronic energy is now labelled 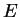 , and the dependence on the
nuclear coordinates is suppressed since the nuclei are assumed to be static
following the conclusions of section 2.2. This equation is an
eigenvalue equation for a linear Hermitian operator, and as such can
always be recast in the form of finding the stationary points of a functional
subject to a constraint.
, and the dependence on the
nuclear coordinates is suppressed since the nuclei are assumed to be static
following the conclusions of section 2.2. This equation is an
eigenvalue equation for a linear Hermitian operator, and as such can
always be recast in the form of finding the stationary points of a functional
subject to a constraint.
Consider the expectation value of the Hamiltonian
![$\langle E \rangle = E [ \Psi ]$](img141.gif) which is a functional of the wave-function,
and make a small variation to the state-vector:
which is a functional of the wave-function,
and make a small variation to the state-vector:
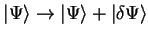 . The change in
. The change in ![$E [ \Psi ]$](img143.gif) is given by
is given by
neglecting changes which are second-order or higher in 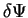 in the
last line. Thus the quantity
in the
last line. Thus the quantity ![$E [ \Psi ]$](img143.gif) is stationary
(
is stationary
(
![$\delta E [ \Psi ] = 0$](img150.gif) ) when
) when
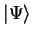 is an eigenstate of
is an eigenstate of 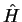 and the eigenvalue is
and the eigenvalue is ![$E [ \Psi ]$](img143.gif) ,
,
![\begin{displaymath}
{\hat H} \vert \Psi \rangle = E [ \Psi ] \vert \Psi \rangle
\end{displaymath}](img151.gif) |
(2.45) |
and this equation is the time-independent Schrödinger equation.
The eigenvalues of 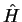 can therefore be found by finding the
stationary values of
can therefore be found by finding the
stationary values of ![$E [ \Psi ]$](img143.gif) i.e. finding the stationary values of
i.e. finding the stationary values of
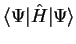 subject to the constraint that
subject to the constraint that
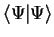 is constant. In this procedure, the eigenvalue
is constant. In this procedure, the eigenvalue
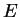 plays the rôle of a Lagrange multiplier used to impose the constraint.
plays the rôle of a Lagrange multiplier used to impose the constraint.
In this dissertation we will only be interested in finding the electronic
ground-state
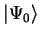 which is the eigenstate of the Hamiltonian
with the lowest eigenvalue
which is the eigenstate of the Hamiltonian
with the lowest eigenvalue 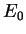 . Suppose that we have a state close to the
ground-state, but with some small error. Since the eigenstates of the
Hamiltonian form a complete set, the error can be expanded as a linear
combination of the excited eigenstates. The whole state can thus be written as
. Suppose that we have a state close to the
ground-state, but with some small error. Since the eigenstates of the
Hamiltonian form a complete set, the error can be expanded as a linear
combination of the excited eigenstates. The whole state can thus be written as
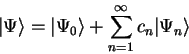 |
(2.46) |
where
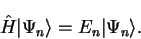 |
(2.47) |
We now calculate the value of ![$E [ \Psi ]$](img143.gif) :
:
By definition, 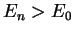 for
for 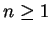 , so that we note two points:
, so that we note two points:
-
![$E [ \Psi ] \geq E_0$](img166.gif) , with
equality only when
, with
equality only when
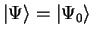 (i.e.
(i.e. 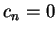 for
for
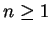 ),
),
- the error in the estimate of
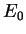 is second-order in the error in
the wave-function (i.e.
is second-order in the error in
the wave-function (i.e. 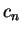 ).
).
The importance of such a variational principle is now clear. To calculate the
ground-state energy 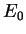 , we can minimise the functional
, we can minimise the functional ![$E [ \Psi ]$](img143.gif) with respect to all states
with respect to all states
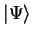 which are antisymmetric under
exchange of particles. The value of this functional gives an upper bound
to the value of
which are antisymmetric under
exchange of particles. The value of this functional gives an upper bound
to the value of 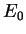 , and even a relatively poor estimate of the ground-state
wave-function gives a relatively good estimate of
, and even a relatively poor estimate of the ground-state
wave-function gives a relatively good estimate of 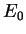 . Eigenstates corresponding to excited states of the Hamiltonian can
be found by minimising the functional with respect to states which are
constructed to be orthogonal to all lower-lying states (which is usually
achieved by considering the symmetries of the states) but in this work we will
only ever be interested in the ground-state, and so there are no restrictions
on the states other than antisymmetry.
. Eigenstates corresponding to excited states of the Hamiltonian can
be found by minimising the functional with respect to states which are
constructed to be orthogonal to all lower-lying states (which is usually
achieved by considering the symmetries of the states) but in this work we will
only ever be interested in the ground-state, and so there are no restrictions
on the states other than antisymmetry.




Next: 3. Quantum Mechanics of
Up: 2. Many-body Quantum Mechanics
Previous: 2.3 Identical particles
Contents
Peter Haynes
![]() as the expectation value of the observable
corresponding to the operator
as the expectation value of the observable
corresponding to the operator ![]() . In that section, mention was briefly
made of the relationship:
. In that section, mention was briefly
made of the relationship:
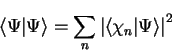
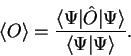
![\begin{displaymath}
{\hat H} \vert \Psi \rangle =
\left[ -\frac{1}{2} \sum_i \n...
...right\vert} \right]
\vert \Psi \rangle = E \vert \Psi \rangle
\end{displaymath}](img140.gif)
![]() which is a functional of the wave-function,
and make a small variation to the state-vector:
which is a functional of the wave-function,
and make a small variation to the state-vector:
![]() . The change in
. The change in ![]() is given by
is given by
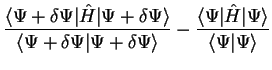
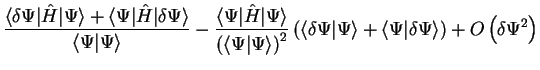
![$\displaystyle \frac{1}{\langle \Psi \vert \Psi \rangle} \left[ \langle \delta \...
...rt \Psi \rangle - E [ \Psi ] \vert \Psi \rangle \right)
\right\}^{\ast} \right]$](img148.gif)
![]() which is the eigenstate of the Hamiltonian
with the lowest eigenvalue
which is the eigenstate of the Hamiltonian
with the lowest eigenvalue ![]() . Suppose that we have a state close to the
ground-state, but with some small error. Since the eigenstates of the
Hamiltonian form a complete set, the error can be expanded as a linear
combination of the excited eigenstates. The whole state can thus be written as
. Suppose that we have a state close to the
ground-state, but with some small error. Since the eigenstates of the
Hamiltonian form a complete set, the error can be expanded as a linear
combination of the excited eigenstates. The whole state can thus be written as
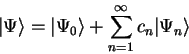
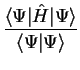
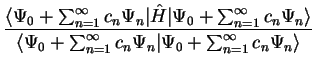
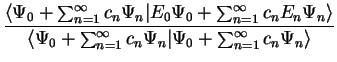
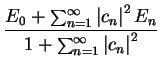
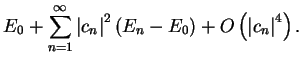
![]() , we can minimise the functional
, we can minimise the functional ![]() with respect to all states
with respect to all states
![]() which are antisymmetric under
exchange of particles. The value of this functional gives an upper bound
to the value of
which are antisymmetric under
exchange of particles. The value of this functional gives an upper bound
to the value of ![]() , and even a relatively poor estimate of the ground-state
wave-function gives a relatively good estimate of
, and even a relatively poor estimate of the ground-state
wave-function gives a relatively good estimate of ![]() . Eigenstates corresponding to excited states of the Hamiltonian can
be found by minimising the functional with respect to states which are
constructed to be orthogonal to all lower-lying states (which is usually
achieved by considering the symmetries of the states) but in this work we will
only ever be interested in the ground-state, and so there are no restrictions
on the states other than antisymmetry.
. Eigenstates corresponding to excited states of the Hamiltonian can
be found by minimising the functional with respect to states which are
constructed to be orthogonal to all lower-lying states (which is usually
achieved by considering the symmetries of the states) but in this work we will
only ever be interested in the ground-state, and so there are no restrictions
on the states other than antisymmetry.