The theory of quantum mechanics is built upon the fundamental concepts of wave-functions and operators. The wave-function is a single-valued square-integrable function of the system parameters and time which provides a complete description of the system. Linear Hermitian operators act on the wave-function and correspond to the physical observables, those dynamical variables which can be measured, e.g. position, momentum and energy.
For systems of atomic nuclei2.1 and electrons, which are
the subject of this dissertation, the system parameters might be taken to be
a set of position variables of the constituent particles (the notation
adopted in this and the following chapters is to refer to electronic variables using a latin index and
nuclear variables with a greek index) i.e.
![]() , their momenta
, their momenta
![]() or even a mixture of the two e.g.
or even a mixture of the two e.g.
![]() . In contrast to a Newtonian system which is
completely described by the positions and momenta of its
constituents, the quantum-mechanical wave-function is a function of only
one of these parameters per particle2.2. The wave-function for the system is thus
typically
denoted by
. In contrast to a Newtonian system which is
completely described by the positions and momenta of its
constituents, the quantum-mechanical wave-function is a function of only
one of these parameters per particle2.2. The wave-function for the system is thus
typically
denoted by
![]() .
.
A notation due to Dirac [4] is often employed, which reflects the
fact
that this wave-function is simply one of many representations of a single
state-vector in a Hilbert space, which is written as
![]() ,
known as
a ket. There also exists a dual space containing a set of
bra vectors, denoted
,
known as
a ket. There also exists a dual space containing a set of
bra vectors, denoted
![]() , defined by their scalar
products and in one-to-one correspondence with the kets.
The scalar product is written as a braket and is anti-linear in the
first argument and linear in the second: thus
, defined by their scalar
products and in one-to-one correspondence with the kets.
The scalar product is written as a braket and is anti-linear in the
first argument and linear in the second: thus
![]() .
It is worth noting here that state-vectors which differ only by
a multiplicative non-zero complex constant describe the same state: we can thus
restrict our interest to the set of normalised vectors defined such
that the scalar product of the vector with its own conjugate equals unity:
.
It is worth noting here that state-vectors which differ only by
a multiplicative non-zero complex constant describe the same state: we can thus
restrict our interest to the set of normalised vectors defined such
that the scalar product of the vector with its own conjugate equals unity:
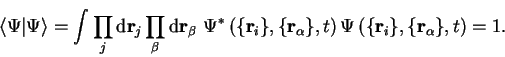 |
(2.1) |
The operator corresponding to some observable ![]() is often written
is often written ![]() ,
and in general when this operator acts on some state-vector
,
and in general when this operator acts on some state-vector
![]() ,
a different (not necessarily normalised) state-vector
,
a different (not necessarily normalised) state-vector
![]() results:
results:
| (2.2) |
The postulates of quantum mechanics [5] state that for a
system in state
![]() :
:
Much of the power of the theory comes from the fact that the quantum-mechanical
states can be linearly superposed since this leads to no ambiguity in the action
of linear operators2.5.
We now consider the quantity
![]() . From Sturm-Liouville theory, the eigenstates of the
operator
. From Sturm-Liouville theory, the eigenstates of the
operator ![]() form a complete set, which means that any valid
state-vector can be expressed as a linear superposition of those
eigenstates with appropriate complex coefficients
form a complete set, which means that any valid
state-vector can be expressed as a linear superposition of those
eigenstates with appropriate complex coefficients ![]() :
:
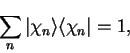 |
(2.7) |
Now this result is applied to the quantity
![]() :
:
| (2.10) |
Since the only possible outcomes of a measurement of the observable ![]() corresponding to operator
corresponding to operator ![]() are the eigenvalues
are the eigenvalues
![]() ,
with corresponding probabilities
,
with corresponding probabilities
![]() (2.4), the quantity
(2.4), the quantity
![]() is to be interpreted as the
expectation value of
is to be interpreted as the
expectation value of ![]() for a system in state
for a system in state
![]() .
The normalisation condition
.
The normalisation condition
![]() corresponds to
the condition that the probabilities sum to unity.
corresponds to
the condition that the probabilities sum to unity.
The final postulate of quantum mechanics states that between measurements, the state-vector
evolves in time according to the time-dependent Schrödinger
equation2.6:
| (2.11) |
Finally we note that if we solve the time-independent Schrödinger
equation, the eigenvalue equation for the Hamiltonian, then the
time-dependence of the wave-function takes a particularly simple form. The
following separation of variables is made:
| (2.13) |
| (2.16) |
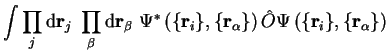 |
|||
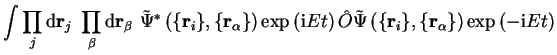 |
|||
| (2.17) |