Michel Côté, Peter D. Haynes and Carla Molteni
Theory of Condensed Matter, Cavendish Laboratory, Madingley Road, Cambridge, CB3 0HE, UK
Modern electronic devices are increasingly being designed by combining materials with different electronic properties. The conventional semiconductor industry has achieved this by building heterostructures, such as quantum wells and superlattices, from materials with the same crystal structure but different constituent atoms. We propose that boron nitride polymers with the same structure as organic polymers will allow the same idea to be applied to polymer materials, already recognised as a cheap alternative to inorganic semiconductors. We demonstrate the similarity between organic polymers and their boron nitride analogues and then explore the potential innovations, including band gap tuning, that these new polymers could bring to organic polymer research.
71.20.Rv, 61.82.Pv, 71.15.Mb, 71.15.Hx
In recent years the electronic properties of polymers have been the subject of intense research because of the potential application of these materials as alternatives to conventional semiconductors for building low-cost electronic devices.
Current research focuses on conjugated organic polymers, which have a
delocalised ![]() -electron system along the carbon
backbone[1]. The choice of organic polymer used in a
particular electronic application is determined by the need to obtain
the desired properties (such as the band gap), which generally depend
upon the arrangement of the constituent carbon atoms. On the other
hand, the semiconductor industry achieves this by exploiting materials
with the same crystalline structure but made of different atoms
(e.g. the IV, III-V and II-VI semiconductors such as Si, GaAs and
ZnSe). Thin layers of materials with different gaps (e.g. GaAs and
AlAs) can also be alternated to form superlattices and quantum wells
where electrons and holes are confined in the region of narrow gap
material; this allows tuning of the band gap to desired values by
varying the heterostructure parameters (e.g. layer thickness) and the
constituent materials. Band gap engineering in conventional
semiconductors has dramatically expanded the range of possible
applications for electronic devices.
-electron system along the carbon
backbone[1]. The choice of organic polymer used in a
particular electronic application is determined by the need to obtain
the desired properties (such as the band gap), which generally depend
upon the arrangement of the constituent carbon atoms. On the other
hand, the semiconductor industry achieves this by exploiting materials
with the same crystalline structure but made of different atoms
(e.g. the IV, III-V and II-VI semiconductors such as Si, GaAs and
ZnSe). Thin layers of materials with different gaps (e.g. GaAs and
AlAs) can also be alternated to form superlattices and quantum wells
where electrons and holes are confined in the region of narrow gap
material; this allows tuning of the band gap to desired values by
varying the heterostructure parameters (e.g. layer thickness) and the
constituent materials. Band gap engineering in conventional
semiconductors has dramatically expanded the range of possible
applications for electronic devices.
Carbon and boron nitride (BN) share many common structures, e.g.
diamond and cubic BN, and the graphitic forms of carbon and BN.
Nanotubes can also be made using these two
compounds[2,3]. Since in those structures, two
carbon atoms are replaced by one boron and one nitrogen atom, it is
worth investigating whether this substitution is also possible in
organic polymers. In fact borazine, a BN analogue of the benzene ring,
a common building block of polymers, does exist and is easily
synthesised. Among the carbon-based structures where ![]() -bonding
plays an important role, conjugated polymers can be ranked between
benzene and graphite in terms of their dimensionality. These two
extremes exist as BN compounds, which suggests that BN polymers could
also be formed. Recently, borazine-based polymers have indeed been
synthesised with a structure equivalent to the carbon polymer
poly(p-phenylene); for reviews on BN polymers see
Ref.[4,5]. The experimental work on BN polymers has
so far focused on finding good precursors to BN ceramics. However, BN
polymers might have other potential applications and advantages
derived from their electronic properties, which, to the best of our
knowledge, have not yet been investigated. The substitution of carbon
by boron and nitrogen in polymers is analogous to making a III-V
compound out of a group-IV semiconductor, which does not change the
structure of the material but only its electronic properties. It is
therefore appealing to see how the electronic properties can be
tailored when BN polymers are combined with their carbon
counterparts. In this Letter, we focus our study on two structures
based on carbon polymers, poly(p-phenylene) and poly(p-phenylenevinylene), whose structures are sketched in
Fig. 1, as examples of how this can be achieved and of the
properties that can be obtained.
-bonding
plays an important role, conjugated polymers can be ranked between
benzene and graphite in terms of their dimensionality. These two
extremes exist as BN compounds, which suggests that BN polymers could
also be formed. Recently, borazine-based polymers have indeed been
synthesised with a structure equivalent to the carbon polymer
poly(p-phenylene); for reviews on BN polymers see
Ref.[4,5]. The experimental work on BN polymers has
so far focused on finding good precursors to BN ceramics. However, BN
polymers might have other potential applications and advantages
derived from their electronic properties, which, to the best of our
knowledge, have not yet been investigated. The substitution of carbon
by boron and nitrogen in polymers is analogous to making a III-V
compound out of a group-IV semiconductor, which does not change the
structure of the material but only its electronic properties. It is
therefore appealing to see how the electronic properties can be
tailored when BN polymers are combined with their carbon
counterparts. In this Letter, we focus our study on two structures
based on carbon polymers, poly(p-phenylene) and poly(p-phenylenevinylene), whose structures are sketched in
Fig. 1, as examples of how this can be achieved and of the
properties that can be obtained.
We have carried out density-functional theory (DFT) calculations using
a pseudopotential total-energy scheme for periodic systems in which
the wavefunctions are expanded in a plane-wave basis[6]. The
local-density approximation (LDA) [7,8] is made
for the exchange-correlation energy. Troullier-Martins
pseudopotentials[9] are used for the boron, carbon and
nitrogen atoms and a modified Kerker pseudopotential[10]
for hydrogen. A cutoff of 60 Ry is employed for the plane-wave
expansion. The polymers are modelled in a periodic cell with a large
distance between neighboring chains to minimize their
interaction. Eight ![]() -points were used for the sampling of the
Brillouin zone. The length of the cell as well as the atomic
coordinates are fully relaxed exhausting all structural degrees of
freedom except for the torsion angle between monomers.
-points were used for the sampling of the
Brillouin zone. The length of the cell as well as the atomic
coordinates are fully relaxed exhausting all structural degrees of
freedom except for the torsion angle between monomers.
Poly(p-phenylene) (PPP) is constructed by concatenating benzene rings. To form the equivalent BN polymer, poly(p-borazylene) (PBZ), the benzene rings are replaced by borazine rings. We can carry out the analogous substitution of carbon atoms by boron and nitrogen in poly(p-phenylenevinylene) (PPV) to get the BN polymer, poly(p-vinyleneborazylene) (PVB). Comparison of the charge densities of the carbon and BN polymers clearly reveals the polarity of the B-N bonds.
To investigate the energetics of these different structures, we have calculated their total binding energies with respect to their constituent atoms. Table I shows the calculated average bond energies, defined as the total binding energy divided by the number of bonds in the structure. In the carbon systems, the carbon atoms in benzene are all equivalent, each bonded to two neighbouring carbon atoms and one hydrogen atom, whereas in graphite every carbon atom is bonded to other carbon atoms. In the polymers PPP and PPV, carbon atoms in both kinds of bonding environment are found. In the BN system, there are more kinds of bonding environment since three species are now involved. The calculated average bond energies for the BN systems show the same trend as the carbon systems. The benzene and borazine molecules have only slightly lower bond energies than their respective graphitic forms. The bond energies of the two polymers considered fall in between these extremes reflecting their mix of bonding environment. These results suggest that the chemistry of the BN polymers should be similar to that of the carbon polymers.
In experiments, PBZ was found to be soluble in ethers[11] whereas PPP is known to be insoluble. This is certainly related to the fact that the BN polymers have polar bonds and are therefore more readily soluble than the non-polar carbon polymers. For insoluble polymers, side chains must be attached to the backbone of the polymer in order to make it soluble: this may lead to complex systems difficult to process. The fact that BN polymers may already be soluble is a desirable property which would facilitate the formation of films from solution in the making of a device. Moreover, if no side chains were needed, the polymers would have more freedom to align which often leads to sharper features in the electronic spectra and higher mobility.
Along with stability and increased processibility, the electronic properties of these polymers represent an important aspect for device application. In general, BN compounds tend to have larger energy gaps than their carbon analogues due to the polarity of the chemical bonds. This effect is seen when the band gaps of group-IV semiconductors are compared to those of III-V and II-VI semiconductors. The same also occurs for first row elements, e.g. cubic BN has a larger band gap than diamond, and graphitic BN is a wide gap insulator whereas graphite is a semimetal. We therefore expect the same behaviour in the polymers. In Figs. 2 and 3 the band structures from the Kohn-Sham eigenvalues obtained in our calculations are plotted. To quantitatively describe the absorption spectra of polymers, the electron-hole interaction, which leads to the formation of excitons, needs to be considered[12,13]. However, the comparison of these band structures (even though they do not include this interaction) should still capture the crucial qualitative features of these systems, as confirmed in BN nanotube calculations[14]. The Kohn-Sham eigenvalues are known to underestimate the band gap, as can be seen from our results for PPV for which we obtain a Kohn-Sham gap of 1.2 eV whereas the known optical gap is 2.5 eV[1]. However, the error does not scale with the magnitude of the gap and it is usually less for large band gap compounds.
The band gaps of the BN polymers are indeed much larger than those of
the equivalent carbon systems and, when the electron-hole interaction
is accounted for, are expected to be in the UV region of the spectrum.
There is also an energy gap in the occupied states for the BN system
which is typical of compounds made from two different elements. In
PBZ, the conduction states at ![]() and at X have the same energy
which means that we cannot rule out the possibility of an indirect gap
in this polymer, whereas the PPP system has a direct gap at
and at X have the same energy
which means that we cannot rule out the possibility of an indirect gap
in this polymer, whereas the PPP system has a direct gap at
![]() . There is also less dispersion in the states near the Fermi
level in PVB than in PPV. These differences and the large gaps will
affect the interaction between electrons and holes and will lead to
differences in the absorption spectra of the carbon and BN polymers.
. There is also less dispersion in the states near the Fermi
level in PVB than in PPV. These differences and the large gaps will
affect the interaction between electrons and holes and will lead to
differences in the absorption spectra of the carbon and BN polymers.
There is an interest per se in wide gap materials, as testified for example by the rapidly developing research on GaN. Pure BN polymers will have band gaps even larger than GaN making them suitable candidate materials for ultraviolet detectors and emitters.
Current research focuses mainly on polymers with band gaps smaller than our forecasts for BN polymers. However, it is desirable to have polymers with band gaps spanning the whole spectral range, from infrared to ultraviolet, thus expanding the possibilities for applications. For this purpose, one can consider combining carbon and BN monomers in the same chain to form a one-dimensional superlattice or copolymer. By analogy with conventional semiconductor superlattices and quantum wells, we expect to be able to tune the gap by changing the lengths of the BN and carbon segments in the copolymer. Copolymers derived from borazine and silazane have been successfully synthesised[15] for use as precursors to SiNCB ceramics. Here we focus on the electronic properties of carbon and BN copolymers, and investigate how polymers made of a mixture of organic and inorganic monomers perform. It is indeed possible to obtain a range of optical gaps using conjugated chains of different lengths or polymers in which the conjugation is broken by adding different components. The systems suggested here have the advantage that the structure of the polymer is essentially the same over its entire length. Given the difference in band gap between the carbon and BN systems, the range of band gap tuning will be fairly large, thus covering a larger region of the spectrum and thus being of interest for a wide range of applications.
|
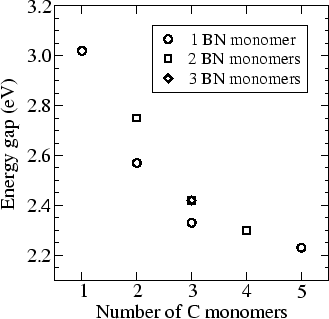
The tuning of the band gap is demonstrated in Fig. 4, where the calculated energy gaps for copolymers of PPP and PBZ are shown as a function of the number of PPP monomers. There are three sets of data differing in the number of BN monomers in between the carbon regions. All the energy gaps of these copolymers lie in between the pure PPP and PBZ values (1.81 and 4.66 eV respectively if calculated within DFT-LDA). Again we should keep in mind the underestimation of the energy gap, due to our neglect of the electron-hole interaction. However, the tuning trend is qualitatively clear. Incidentally, the calculated energy cost for the formation of the copolymers is about 1 eV per unit cell which reflects the cost involved in the formation of the C-B and C-N bonds.
The BN monomer lacks inversion symmetry and this will result in polarisation in both the ground and excited states. This becomes apparent when the states near the Fermi level are visualised. The highest occupied state resides mostly in the carbon region but is weighted towards the end bonded to the nitrogen atom with significant weight also on the nitrogen. On the other hand, the lowest unoccupied state is weighted towards the opposite end of the region near the boron atom. The presence of a dipole moment indicates possible enhanced non-linear optical effects. Inversion symmetry may be restored to the copolymer by alternating the orientation of consecutive BN regions, thus doubling the unit cell and creating two inequivalent carbon regions, one terminated by a boron atom at each end and the other by nitrogen atoms. In this case, we will also have separation of electrons and holes since they will reside in the different carbon regions.
In many applications, it is desirable to mix carbon and BN polymers in
the solid state. In the case of the graphitic forms of carbon and BN,
the interactions between the sheets are known to be comparable with
similar interlayer spacings in graphite, graphitic BN and in mixtures
of these compounds, as has been seen in nanoparticles and nanotubes
made out of sheets of the two compounds[16]. There are
also indications[17] that the solid phase of PBZ consists
of a layered structure with spacings between 3.4-3.7 Å, which
suggests a similar interaction to that in the conjugated carbon
polymers. To further complement our study, we have calculated the
structural and electronic properties of the crystal phases of a
mixture of carbon and BN polymers. Since the unit cell lengths of
carbon and BN polymers are very similar, they can be combined in the
same crystal. We started from the crystal structures of the pure
carbon phases, because we believe that the inter-chain interactions
are similar. For PPP, we used the orthorhombic crystal (space group
![]() ) which has two polymer chains in its primitive cell and we
replaced one of these by its BN equivalent. We did not consider the
twisting angle between adjacent monomers which is seen in experiment
since it is found to be energetically indistinguishable in our
calculations. For PPV, we used the monoclinic structure with symmetry
) which has two polymer chains in its primitive cell and we
replaced one of these by its BN equivalent. We did not consider the
twisting angle between adjacent monomers which is seen in experiment
since it is found to be energetically indistinguishable in our
calculations. For PPV, we used the monoclinic structure with symmetry
![]() . Upon relaxation of the lattice parameters and atomic
coordinates, using a
. Upon relaxation of the lattice parameters and atomic
coordinates, using a
![]()
![]() -point grid, we found
no significant deviation from the initial configurations, i.e. the
chains remained separated with little change in the volume of the
cell.
-point grid, we found
no significant deviation from the initial configurations, i.e. the
chains remained separated with little change in the volume of the
cell.
|
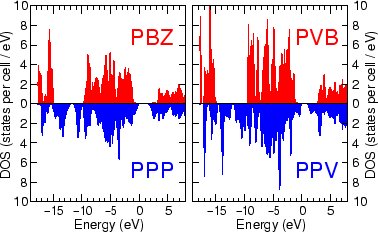
Fig. 5 shows the electronic densities of states for both crystals, decomposed by projection into separate contributions from the different chains. The states on the BN chain are shown by the upper curve and the states on the carbon chain are shown by the inverted lower curve. There are no states on the BN polymers in a region between -15 and -10 eV which is characteristic of the polar compound. The energy gap between occupied and unoccupied states is larger for the BN chain than for the carbon chain. It is also interesting how the states line up near the Fermi level. On both the occupied and unoccupied sides of the gap, the carbon states are closer to the Fermi level than the BN states and this indicates that electrons and holes in these mixed solids will reside predominately on the carbon polymers. We therefore expect larger ionisation energies and lower electron affinities for the BN polymers than for the carbon polymers. These properties might be used in a mixed device of carbon and BN polymers in which holes can be injected into the BN system and then transferred to the carbon system.
In conclusion, our study demonstrates the potential innovations of using BN polymers, particularly in combination with organic polymers with the same structure. The BN polymers have larger gaps than their carbon counterparts and are therefore relevant for applications in a different spectral range. However, when BN and carbon polymers are combined in one-dimensional heterostructures, the band gap can be tailored to a desired value over a wide range, in a similar manner to what is done in conventional semiconductor heterostructures. While BN polymers are currently synthesised for other purposes, e.g. as precursors to ceramics, a better understanding of their electronic properties opens new possibilities for the making of non-conventional electronic devices.