 |
 |
A chlorine molecule of bond length 2.0 Å is placed in a cubic box of
side 10 Å. With a cutoff energy of 640 eV and the basis-function
radius ![]() of 4.0 Å, a
total of
of 4.0 Å, a
total of
![]() basis functions are used.
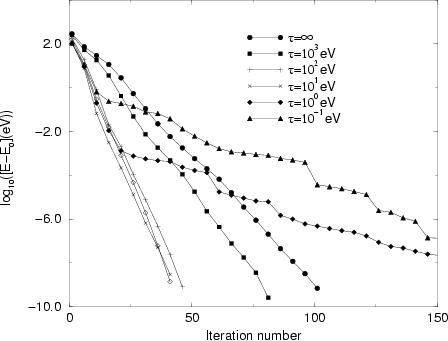
In Fig. 1 we display
the convergence of the sum of Kohn-Sham eigenvalues toward the
``exact'' value obtained from direct matrix diagonalization, as a
function of the iteration number. The convergence of solution is seen
to be linear when the number of iterations is smaller than the number
of basis functions. To investigate the effect of preconditioning on
the convergence of the solution, we have used a number of fixed
basis functions are used.
In Fig. 1 we display
the convergence of the sum of Kohn-Sham eigenvalues toward the
``exact'' value obtained from direct matrix diagonalization, as a
function of the iteration number. The convergence of solution is seen
to be linear when the number of iterations is smaller than the number
of basis functions. To investigate the effect of preconditioning on
the convergence of the solution, we have used a number of fixed ![]() values. It is seen that the performance of the method improves with
moderate preconditioning.
Fig. 1 shows that
values. It is seen that the performance of the method improves with
moderate preconditioning.
Fig. 1 shows that ![]() should be about 10 eV for good
convergence. We have performed another calculation with
should be about 10 eV for good
convergence. We have performed another calculation with ![]() updated according to the highest kinetic energy of all approximate
eigenvectors, which converges to 24 eV. This is the natural choice
for
updated according to the highest kinetic energy of all approximate
eigenvectors, which converges to 24 eV. This is the natural choice
for ![]() used in other preconditioning schemes, and the performance
of this calculation (the curve labelled by open diamonds
used in other preconditioning schemes, and the performance
of this calculation (the curve labelled by open diamonds ![]() )
is seen to be rather similar to that of the `optimal' case with
)
is seen to be rather similar to that of the `optimal' case with ![]() eV. This method therefore allows
eV. This method therefore allows ![]() to be chosen
automatically, and optimized during the calculation, rather than being
another parameter which the user must specify.
to be chosen
automatically, and optimized during the calculation, rather than being
another parameter which the user must specify.
 |
To investigate the importance of preserving the tensor nature of
the search direction, we have performed calculations with the same
cutoff energy of 640 eV on the molecular chlorine system, but this
time with ![]() set to the identity matrix (this corresponds to the case
where tensor nature of the search direction is not preserved) and the
off-diagonal elements of
set to the identity matrix (this corresponds to the case
where tensor nature of the search direction is not preserved) and the
off-diagonal elements of ![]() set to zero (this corresponds to the
diagonal approximation used in Ref. [14]) when we solve
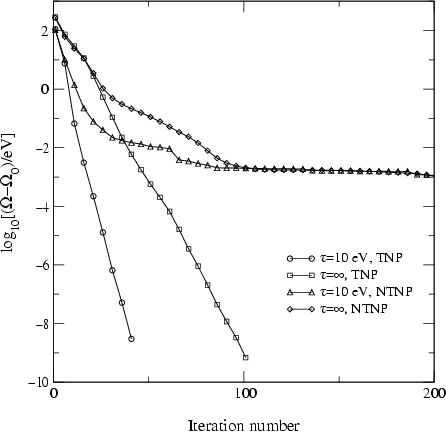
Eq. 22. The results of the calculations are presented
in Fig. 2 where we have included the
tensor-nature-preserving (TNP) curves for comparison. It is found that
that the non-tensor-property-preserving (NTNP) cases fail to converge
to the right solution. We conclude that it is essential to take
tensor properties into account when one is dealing with a
non-orthogonal basis set.
set to zero (this corresponds to the
diagonal approximation used in Ref. [14]) when we solve
Eq. 22. The results of the calculations are presented
in Fig. 2 where we have included the
tensor-nature-preserving (TNP) curves for comparison. It is found that
that the non-tensor-property-preserving (NTNP) cases fail to converge
to the right solution. We conclude that it is essential to take
tensor properties into account when one is dealing with a
non-orthogonal basis set.
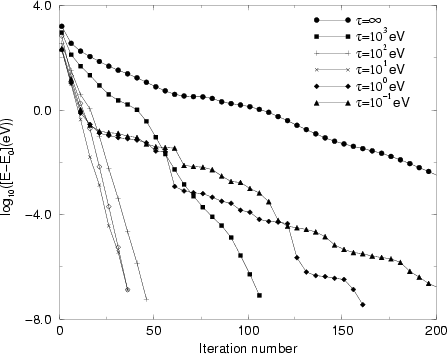 |
With a cutoff energy as high as 4800 eV (a total of
![]() basis functions are used in these calculations),
Fig. 3 clearly indicates that it is crucial to use
the preconditioning scheme. A comparison between
Figs. 1 and 3 reveals that when
the optimal value of
basis functions are used in these calculations),
Fig. 3 clearly indicates that it is crucial to use
the preconditioning scheme. A comparison between
Figs. 1 and 3 reveals that when
the optimal value of ![]() is used, the number of iterations to achieve
the same accuracy remains roughly the same, even though the number of
basis functions has more than doubled, which shows that the
preconditioning scheme is indeed working.
is used, the number of iterations to achieve
the same accuracy remains roughly the same, even though the number of
basis functions has more than doubled, which shows that the
preconditioning scheme is indeed working.
 |
Similar tests are performed on the bulk crystalline silicon system.
The calculations on a 64-atom silicon unit cell are performed at
the equilibrium lattice parameter of 5.43 Å with an energy cutoff
of 200 eV. We have chosen ![]() to be 3.1
Å which is sufficient for this purpose.
These settings result in a total of
to be 3.1
Å which is sufficient for this purpose.
These settings result in a total of
![]() basis
functions for the calculations.
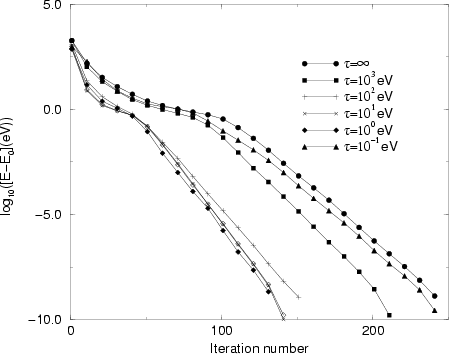
In Fig. 4 we
we note that our `best'
basis
functions for the calculations.
In Fig. 4 we
we note that our `best' ![]() eV is
comparable with the value of 3.8 eV used by Bowler and Gillan
[14]. We have performed another calculation with
eV is
comparable with the value of 3.8 eV used by Bowler and Gillan
[14]. We have performed another calculation with ![]() updated according to the highest kinetic energy of all approximate
eigenvectors, which converges to 12 eV. The performance of
this calculation is seen to be rather similar to that of the optimal
cases with
updated according to the highest kinetic energy of all approximate
eigenvectors, which converges to 12 eV. The performance of
this calculation is seen to be rather similar to that of the optimal
cases with ![]() or 10 eV.
or 10 eV.