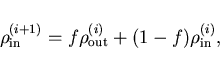

Next: 3. The iterative method
Up: Preconditioned conjugate gradient method
Previous: 1. Introduction
2. Formulation of the problem
We give a brief account of electronic structure calculations within
density-functional theory [16] which requires
the generalized eigenvalue problem to be solved (see Ref. [17] for a more comprehensive description). For a
system of 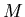 electrons, we need to solve self-consistently the
Kohn-Sham equations which assume the following form
electrons, we need to solve self-consistently the
Kohn-Sham equations which assume the following form
![\begin{displaymath}
\hat{H} \psi_m({\bf r}) = \left[-\frac{\hbar^2}{2m_{\mathrm ...
...f r}) \right] \psi_m({\bf r}) =
\varepsilon_m \psi_m({\bf r}),
\end{displaymath}](img12.gif) |
(1) |
where 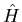 is the Kohn-Sham Hamiltonian, with energy eigenvalues
is the Kohn-Sham Hamiltonian, with energy eigenvalues
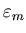 and corresponding eigenstates
and corresponding eigenstates
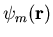 . The
effective potential
. The
effective potential
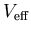 consists of three terms; the
classical electrostatic or Hartree potential, the exchange-correlation
potential, and the external potential [17]. The
electron density is formed from the
consists of three terms; the
classical electrostatic or Hartree potential, the exchange-correlation
potential, and the external potential [17]. The
electron density is formed from the 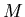 lowest or occupied eigenstates
lowest or occupied eigenstates
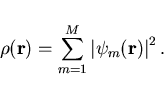 |
(2) |
The eigenstates satisfy the orthogonality constraints where
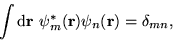 |
(3) |
for all 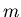 and
and 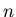 .
.
When a non-orthogonal basis set
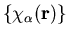 is used, the eigenstates are written as
is used, the eigenstates are written as
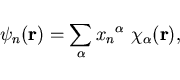 |
(4) |
where 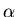 labels a basis function
labels a basis function
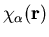 . The
right hand side of Eq. (4) has been written as a
contraction between a contravariant quantity
. The
right hand side of Eq. (4) has been written as a
contraction between a contravariant quantity 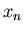 and a covariant
quantity
and a covariant
quantity 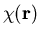 . Substituting Eq. (4) into
Eq. (1), taking inner products with the
. Substituting Eq. (4) into
Eq. (1), taking inner products with the
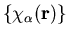 , and using the definitions
, and using the definitions
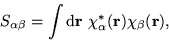 |
(5) |
and
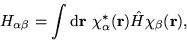 |
(6) |
we obtain the generalized eigenvalue problem
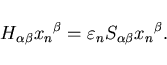 |
(7) |
In writing Eq. (7), we have adopted the Einstein
summation notation where we sum over repeated Greek indices. The
orthogonality conditions of the Kohn-Sham eigenstates in
Eq. (3) translate into
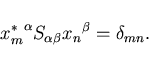 |
(8) |
When Eq. (7) is solved, a new output electron
density
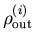 is obtained and a new input
electron density for the next iteration can be constructed by a linear
(or more sophisticated [18]) mixing scheme e.g.
is obtained and a new input
electron density for the next iteration can be constructed by a linear
(or more sophisticated [18]) mixing scheme e.g.
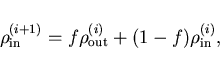 |
(9) |
where the optimum choice for 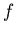 depends upon the eigenvalues of the
static dielectric matrix of the system. The mixing of densities is
carried out until Eq. (1) is solved self-consistently.
depends upon the eigenvalues of the
static dielectric matrix of the system. The mixing of densities is
carried out until Eq. (1) is solved self-consistently.


Next: 3. The iterative method
Up: Preconditioned conjugate gradient method
Previous: 1. Introduction
Peter Haynes
![\begin{displaymath}
\hat{H} \psi_m({\bf r}) = \left[-\frac{\hbar^2}{2m_{\mathrm ...
...f r}) \right] \psi_m({\bf r}) =
\varepsilon_m \psi_m({\bf r}),
\end{displaymath}](img12.gif)
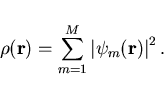
![]() is used, the eigenstates are written as
is used, the eigenstates are written as
![]() is obtained and a new input
electron density for the next iteration can be constructed by a linear
(or more sophisticated [18]) mixing scheme e.g.
is obtained and a new input
electron density for the next iteration can be constructed by a linear
(or more sophisticated [18]) mixing scheme e.g.