

Next: 3. Traditional parallel implementation
Up: Parallel fast Fourier transforms
Previous: 1. Introduction
2. Fast Fourier transforms
For a full description of the FFT see, for example Ref. [5]. We consider a vector of length 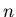 with elements
with elements 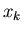 where
where 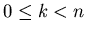 . The elements of the discrete Fourier transform
(DFT) of this vector,
. The elements of the discrete Fourier transform
(DFT) of this vector, 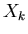 , may then be defined by
, may then be defined by
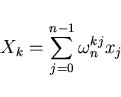 |
(1) |
where 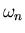 is one of the
is one of the
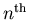 roots of unity
roots of unity
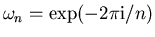 . The definition in Eq. 1
is simply a premultiplication of the vector with elements
. The definition in Eq. 1
is simply a premultiplication of the vector with elements 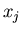 by a
matrix with elements
by a
matrix with elements
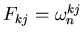 , and this
multiplication requires
, and this
multiplication requires 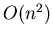 operations.
operations.
Consider the following result, known as the Danielson-Lanczos
lemma [6], applied to Eq. 1 for even 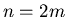 :
:
in which we use the result
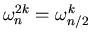 and
introduce the notation
and
introduce the notation
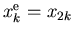 and
and
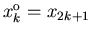 to represent the even and odd elements
respectively. Equation 2 shows that a DFT of length
to represent the even and odd elements
respectively. Equation 2 shows that a DFT of length 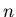 may be
rewritten as the combination of two DFTs of length
may be
rewritten as the combination of two DFTs of length 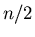 . This lemma
may be applied recursively, as long as the length of the DFT remains
even, so that if
. This lemma
may be applied recursively, as long as the length of the DFT remains
even, so that if 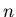 is a power of 2, it may be applied until the
trivial DFT of a vector of length 1 is required. In this case, the DFT
requires only
is a power of 2, it may be applied until the
trivial DFT of a vector of length 1 is required. In this case, the DFT
requires only 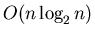 operations, and this is the (radix-2)
FFT. The lemma may be generalised to apply when
operations, and this is the (radix-2)
FFT. The lemma may be generalised to apply when 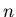 contains factors
other than 2.
contains factors
other than 2.
In three dimensions, the definition of the DFT is
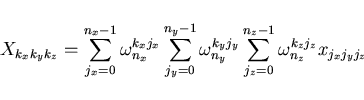 |
(3) |
Equation 3 demonstrates that the three-dimensional DFT is the
product of 3 one-dimensional DFTs which all commute with each other
since they act indepedently.


Next: 3. Traditional parallel implementation
Up: Parallel fast Fourier transforms
Previous: 1. Introduction
Peter Haynes
![]() :
: