

Next: Conclusions
Up: Nonorthogonal generalized Wannier function
Previous: The FFT box technique
The NGWF pseudopotential plane-wave method in practice
We have implemented our method in a new code and we have performed
extensive tests on a variety of systems. We have also performed
comparisons with CASTEP [1], an established
pseudopotential plane-wave code that we use as our point of
reference. We expect our approach to have efficiency comparable to the
traditional cubic-scaling plane-wave pseudopotential method and thus
it would be possible to use it in its place for systems with a band
gap. In that case, a calculation with our method would afford a set of
optimal localised functions which could be used directly in
applications such as the calculation of polarisation changes in
crystalline solids [48,49]. However, the most
important application that we envisage is the extension of the
present formalism to linear-scaling calculations on very large
systems. Such an extension requires the truncation of the density
kernel, an issue which has been already investigated in detail
[33,35,50]. The resulting
linear-scaling method would be directly comparable to and have the
same advantages as the plane-wave approach.
Since we optimise the NGWFs iteratively, some
initial guesses are required for them. In this work
we use pseudo-atomic orbitals (PAOs) that vanish outside
a spherical region [51]. These orbitals are generated
for the isolated atoms with the same radii, norm-conserving
pseudopotentials and kinetic energy cutoff as in our calculations.
Even though these NGWF guesses are optimal for the isolated
atoms, they undergo large changes during our calculations
so that in practice any guess that resembles an atomic orbital could
be used, such as Slater or Gaussian functions.
We first demonstrate the accuracy of the FFT box technique as compared
to using the entire simulation cell as the FFT grid. We define the
quantity
![\begin{displaymath}
\Delta E \equiv E^{\mathrm{box}}[n] - E[n],
\end{displaymath}](img122.png) |
(30) |
where
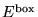 is the total energy per atom calculated using
the FFT box technique and
is the total energy per atom calculated using
the FFT box technique and 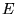 is that calculated using the entire
simulation cell. Figure 2 shows
is that calculated using the entire
simulation cell. Figure 2 shows 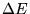 for the butane
molecule (C
for the butane
molecule (C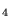 H
H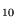 ) for different FFT box sizes. For this test we
used a cubic simulation cell of side length
) for different FFT box sizes. For this test we
used a cubic simulation cell of side length 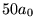 and grid spacing
and grid spacing
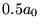 . The PAOs on all the atoms were confined within spherical
regions of radius
. The PAOs on all the atoms were confined within spherical
regions of radius 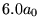 . The carbon atoms had one 2s and three 2p
orbitals and the hydrogen atoms had a single 1s orbital. In this case
the PAOs were not optimised during the calculation.
. The carbon atoms had one 2s and three 2p
orbitals and the hydrogen atoms had a single 1s orbital. In this case
the PAOs were not optimised during the calculation.
Figure 2:
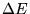 plotted for a butane molecule as a function of FFT
box size. All PAOs were confined to atom centered localisation regions
of radius
plotted for a butane molecule as a function of FFT
box size. All PAOs were confined to atom centered localisation regions
of radius 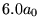 , and the grid spacing was
, and the grid spacing was 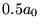 .
.
![\scalebox{0.5}{\includegraphics*[0cm,1cm][26cm,18.5cm]{butane.eps} }](img128.png)
|
It is seen that the error associated with using the FFT box rather
than the entire simulation cell is only of the order of 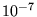 E
E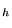 per atom, which is insignificant in the context of DFT
calculations. We also note that the convergence
of the total energy with FFT box size is not strictly variational, as
is expected: as the FFT box size is increased, it is true that the
basis set expands, but the smaller basis is not necessarily a subset
of the larger one. For a given FFT box size, however, the kinetic
energy cutoff of our basis functions (and hence the grid-spacing)
is a variational parameter, just as in traditional plane-wave
DFT. Further tests and discussion of the FFT box technique will be
published elsewhere [47].
per atom, which is insignificant in the context of DFT
calculations. We also note that the convergence
of the total energy with FFT box size is not strictly variational, as
is expected: as the FFT box size is increased, it is true that the
basis set expands, but the smaller basis is not necessarily a subset
of the larger one. For a given FFT box size, however, the kinetic
energy cutoff of our basis functions (and hence the grid-spacing)
is a variational parameter, just as in traditional plane-wave
DFT. Further tests and discussion of the FFT box technique will be
published elsewhere [47].
Our next example involves the potential energy curve of the LiH
molecule inside a large cubic simulation cell of side length 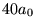 .
.
Figure 3:
Potential energy curves for LiH generated with the
CASTEP plane-wave pseudopotential code and with our method
for NGWF radii of 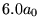 and
and 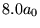 and for s-type PAOs
with a radius of
and for s-type PAOs
with a radius of 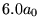 .
.
![\scalebox{0.5}{\includegraphics*[0cm,1cm][25cm,18.5cm]{LiH_potential.eps} }](img132.png)
|
In Figure 3 the potential energy curve is shown as calculated
by CASTEP and by our method with the same kinetic energy cutoff of
538eV.
As we have used norm-conserving Troullier-Martins [52]
pseudopotentials, this is a two electron system which we describe by
one NGWF on each atom. It can be seen that when we use NGWFs with
radii of 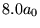 , we have mE
, we have mE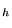 agreement in total energies with
the CASTEP results. Furthermore, the equilibrium bond length and vibrational
frequency for this case differ from the CASTEP results by only -0.19% and
0.74% respectively. For the smaller radius of
agreement in total energies with
the CASTEP results. Furthermore, the equilibrium bond length and vibrational
frequency for this case differ from the CASTEP results by only -0.19% and
0.74% respectively. For the smaller radius of 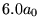 the curve
diverges from the CASTEP curve at large bond lengths. This is because
the NGWF sphere overlap, and therefore the number of delta
functions between the atoms, decreases more rapidly for the small radii
as the atoms are pulled apart. Also shown in the same Figure is a curve that
has been generated with our method but without optimisation of the
NGWFs, which were kept constant and equal to the initial PAO guesses.
This is equivalent to a tight-binding calculation with a minimal PAO
basis. As can be seen, the total energies deviate significantly from
the CASTEP result, as one would expect.
The equilibrium bond length for this case differs by
3.34% from CASTEP, as compared to -1.24% for the
the curve
diverges from the CASTEP curve at large bond lengths. This is because
the NGWF sphere overlap, and therefore the number of delta
functions between the atoms, decreases more rapidly for the small radii
as the atoms are pulled apart. Also shown in the same Figure is a curve that
has been generated with our method but without optimisation of the
NGWFs, which were kept constant and equal to the initial PAO guesses.
This is equivalent to a tight-binding calculation with a minimal PAO
basis. As can be seen, the total energies deviate significantly from
the CASTEP result, as one would expect.
The equilibrium bond length for this case differs by
3.34% from CASTEP, as compared to -1.24% for the 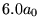 NGWF
calculation. Thus, optimising the NGWFs improves the estimate of the
bond length. The vibrational frequency obtained from the PAO case,
however, differs by 3.51% from CASTEP, as compared to 5.33% for the
NGWF
calculation. Thus, optimising the NGWFs improves the estimate of the
bond length. The vibrational frequency obtained from the PAO case,
however, differs by 3.51% from CASTEP, as compared to 5.33% for the
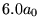 NGWF calculation. This, we believe, is an artefact of the
localisation constraint imposed on the NGWFs and suggests that in fact
localisation radii greater than
NGWF calculation. This, we believe, is an artefact of the
localisation constraint imposed on the NGWFs and suggests that in fact
localisation radii greater than 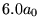 should be used in practice.
should be used in practice.
We now show convergence of the total energy with NGWF radius. For our
tests we have used a silane (SiH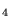 ) molecule with the same
simulation cell and grid spacing as described above. A local Troullier-Martins
[52] norm-conserving pseudopotential was used on the
hydrogen atoms and a non-local one on the silicon atom. The number of
NGWFs on each atom was as many as in the valence shells of the
isolated atoms, i.e. one on hydrogen and four on silicon.
) molecule with the same
simulation cell and grid spacing as described above. A local Troullier-Martins
[52] norm-conserving pseudopotential was used on the
hydrogen atoms and a non-local one on the silicon atom. The number of
NGWFs on each atom was as many as in the valence shells of the
isolated atoms, i.e. one on hydrogen and four on silicon.
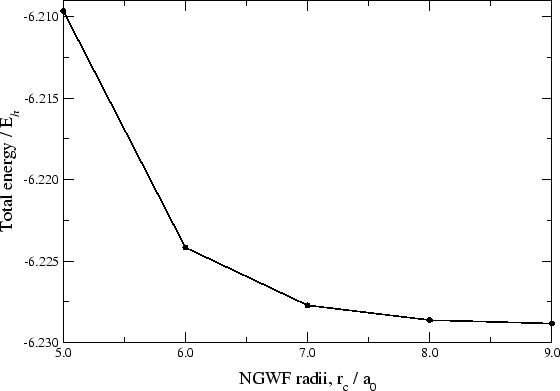
Figure 4:
Total energy of a silane molecule calculated with our method
for various NGWF radii (r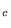 ).
).
|
Figure 4 shows total energy results calculated for this
system as a function of NGWF sphere radii. Convergence is uniform and
to mE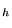 accuracy by the time we get to a radius of
accuracy by the time we get to a radius of 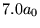 .
Such an NGWF radius should be adequate for practical calculations.
.
Such an NGWF radius should be adequate for practical calculations.
Here we also show that large qualitative changes occur to the shapes
of the NGWFs during optimisation.
In Figure 5 we show plots of isosurfaces of the
NGWFs for an ethene molecule in a large simulation cell,
before and after optimisation. The NGWF radius was 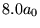 for all atoms.
for all atoms.
In particular, the carbon 2p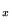 orbital, which is
collinear with the C-C
orbital, which is
collinear with the C-C 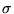 bond, focusses more around this
bond and gains two more lobes and nodes at the positions of the
hydrogen atoms farthest from its carbon centre. The hydrogen
functions, starting from 1s, obtain after optimisation
a complicated shape that extends over the whole molecule and
has nodal surfaces betwen the carbons and the rest of the
hydrogens. The deep qualitative changes to the shapes of
the NGWFs that occur during their optimisation with our method
are obviously necessary for obtaining a plane-wave equivalent
result. Our optimised NGWFs in general look nothing like
the atomic orbitals they started from and are adjusted to
their particular molecular environment.
We therefore conclude that using the delta function
basis set and performing all operations consistently with the
plane-wave formalism is important for obtaining
the systematic convergence that plane-waves have.
bond, focusses more around this
bond and gains two more lobes and nodes at the positions of the
hydrogen atoms farthest from its carbon centre. The hydrogen
functions, starting from 1s, obtain after optimisation
a complicated shape that extends over the whole molecule and
has nodal surfaces betwen the carbons and the rest of the
hydrogens. The deep qualitative changes to the shapes of
the NGWFs that occur during their optimisation with our method
are obviously necessary for obtaining a plane-wave equivalent
result. Our optimised NGWFs in general look nothing like
the atomic orbitals they started from and are adjusted to
their particular molecular environment.
We therefore conclude that using the delta function
basis set and performing all operations consistently with the
plane-wave formalism is important for obtaining
the systematic convergence that plane-waves have.
Our final example demonstrates the direct applicability of
Figure 6:
A portion (Si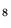 H
H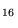 ) of an infinite linear silane chain in a hexagonal
simulation cell.
) of an infinite linear silane chain in a hexagonal
simulation cell.
|
our method to any lattice symmetry without any modification.
This is a consequence of being consistent throughout with the
plane-wave formalism. As we have shown for the calculation
of the kinetic energy in this way [43], we also
achieve better accuracy at no additional cost compared
with a finite difference approach. In Figure 6
we show a portion (Si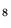 H
H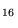 ) of an infinite
linear silane chain inside a hexagonal simulation cell
on which we have performed a total energy calculation
at a kinetic energy cutoff of 183eV. The radii of the
NGWFs were
) of an infinite
linear silane chain inside a hexagonal simulation cell
on which we have performed a total energy calculation
at a kinetic energy cutoff of 183eV. The radii of the
NGWFs were 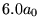 on silicon and
on silicon and 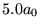 on hydrogen.
A total energy of -39.097E
on hydrogen.
A total energy of -39.097E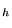 was obtained when we optimised
the density kernel only (with the NGWFs kept constant and
equal to PAOs). When both the density
kernel and the NGWFs were optimised, the energy lowered to
-52.216E
was obtained when we optimised
the density kernel only (with the NGWFs kept constant and
equal to PAOs). When both the density
kernel and the NGWFs were optimised, the energy lowered to
-52.216E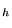 , which is another manifestation
of the fact that both the density kernel and the NGWFs should be
optimised in calculations with our method.
, which is another manifestation
of the fact that both the density kernel and the NGWFs should be
optimised in calculations with our method.


Next: Conclusions
Up: Nonorthogonal generalized Wannier function
Previous: The FFT box technique
Peter D. Haynes
2002-10-31
![]() .
.
![]() ) molecule with the same
simulation cell and grid spacing as described above. A local Troullier-Martins
[52] norm-conserving pseudopotential was used on the
hydrogen atoms and a non-local one on the silicon atom. The number of
NGWFs on each atom was as many as in the valence shells of the
isolated atoms, i.e. one on hydrogen and four on silicon.
) molecule with the same
simulation cell and grid spacing as described above. A local Troullier-Martins
[52] norm-conserving pseudopotential was used on the
hydrogen atoms and a non-local one on the silicon atom. The number of
NGWFs on each atom was as many as in the valence shells of the
isolated atoms, i.e. one on hydrogen and four on silicon.
![]() for all atoms.
for all atoms.