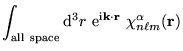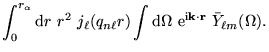

Next: 4. Overlap matrix elements
Up: Localised spherical-wave basis set
Previous: 2. Origin of the
We define the Fourier transform of a basis function
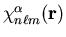 by
by
The angular integral is performed by using the expansion of
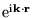 into spherical-waves
(42, Appendix) leaving the radial integral
into spherical-waves
(42, Appendix) leaving the radial integral
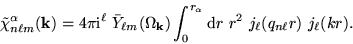 |
(8) |
The radial integral can now be calculated using equations
(43,44) given in the Appendix and the
boundary conditions (that the basis functions are finite at 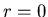 and vanish at
and vanish at
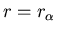 ) for the cases when
) for the cases when
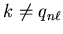 and
and
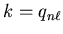 respectively. The final result for the
Fourier transform of a basis function is then
respectively. The final result for the
Fourier transform of a basis function is then
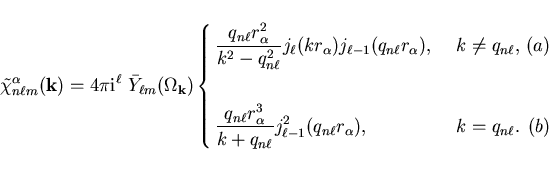 |
(9) |
Equation (9b) is in fact a limiting case of
(9a) which can therefore always be substituted for
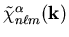 in an integral over
reciprocal-space.
in an integral over
reciprocal-space.


Next: 4. Overlap matrix elements
Up: Localised spherical-wave basis set
Previous: 2. Origin of the
Peter Haynes