In previous work [33, 50] VMC and DMC
calculations were performed on diamond-structure germanium using the
techniques described in chapter 
, but variance
minimisation was not used to optimise the function in those
calculations. The VMC calculations described in Refs.[33, 50] were repeated using the optimised functions described
above. A fcc simulation cell of diamond structure germanium
containing 16 atoms was studied. The single particle orbitals were
obtained from a LDA calculation using a plane-wave basis set
containing all plane waves up to a kinetic energy cutoff of 40 Ry. The
calculations were performed at a non-zero wavevector of the simulation
cell Brillouin zone using the techniques described in
chapter and Refs.[33, 50].
The first set of calculations used a function containing 6 stars of
vectors, whose coefficients had been optimised by the variance
minimisation procedure, described in this chapter. The second set of
optimisations of were performed again with 6 stars of vectors
and with a further 6 parameters in the g(r) function (5 for
to 
and B). 10,000 configurations were used in
both the optimisations. The configurations for the second
optimisation were generated from a VMC calculation using the best from the first optimisation. Values of L=3.0, 3.5, 4.0, 5.0 were used
for the range of the g(r) function. The results yielding the lowest
variance of the local energy are illustrated in figure .
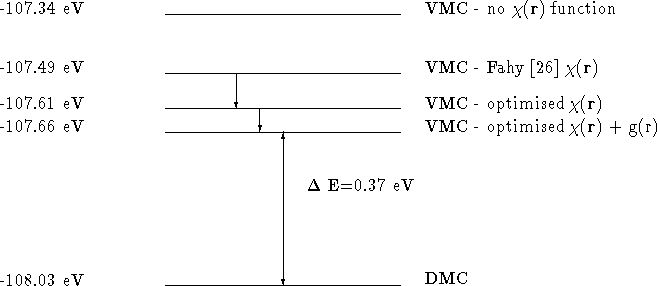
Figure: Reduction in energy from optimising the function and adding g(r) to the function.
This figure shows that the introduction of a function according to the Fahy prescription, lowers the total energy by 0.15 eV per atom. Optimising the values of the coefficients in this function using the variance minimisation scheme lowers the energy by a further 0.17 eV per atom. The introduction of g(r) reduces the VMC energy by at most a further 0.05 eV per atom. The variance of the energy is only reduced by a few percent during the whole optimisation process.