As well as calculating energy gaps, it is also possible to calculate a
band width via indirect excitations. In figure 
, two
sets of excitations are shown for calculating the width of the valence
band at the 
-point.
Figure: Indirect excitations to
calculate the width of the valence band at the -point.
Excitations from 
are shown in red and from
are shown in blue. The black lines represent a
pseudopotential bandstructure[94].
The band width can be calculated as the difference in energy between
exciting from the bottom of the valence band at to the
bottom of the conduction band at X or L and exciting from the top of
the valence band at to the bottom of the conduction band at X
or L,
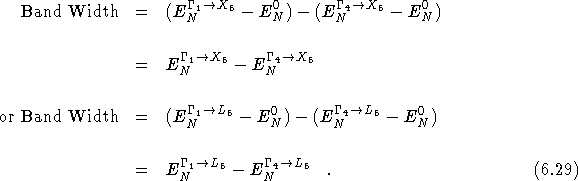
where 
represents the energy of the
state where the orbital in the Slater determinant representing the top
of the valence band at the -point( 
) has been
replaced by one representing the bottom of the conduction band at the
L-point( 
). The results of these DMC calculations of the band
width are shown in table . The n=2 LDA and HF
band widths have been included for comparison. As with excitation
energies the LDA band widths contain a very small finite size effect.
The fully converged HF result for the band width is 18.5 eV[112].
The DMC results show a reasonable agreement with experiment, if not quite within error bars. As with the ordinary excitations, the DMC again overestimates the size of the band width. This overestimation could be due to the inferior quality of the nodal structure of the guiding wavefunction for the excitation from the bottom of the valence band to the bottom of the conduction band or to finite size effects.
1  Promotion | 2  Promotion | DMC (eV) | Expt. (eV) | LDA (eV) | HF (eV) |
 |  | 13.3 
0.6 | 12.5 | 12.03 | 16.2 |
 |  | 14.1
0.6 | 12.5 | 12.03 | 16.2 |
band at the