


Next: Promoting Electrons
Up: Addition and Subtraction of
Previous: Addition and Subtraction of
As DMC calculations are considerably more computationally expensive
than VMC calculations, only a selected set of the VMC results were
repeated in DMC. It was decided to use the addition and removal
of electrons at the 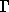 -point as a test for comparing the DMC
with VMC and experiment. Two separate modifications to the DMC
algorithm were experimented with,
-point as a test for comparing the DMC
with VMC and experiment. Two separate modifications to the DMC
algorithm were experimented with,
- DMC calculations were performed using the original Ewald
expression for the electron-electron interaction and the new version
of the interaction described in section
 .
. - DMC calculations were performed using single-particle orbitals
in the Slater determinant from LDA calculations where the orbitals are
kept fixed when an electron is added or removed and where the orbitals
are allowed to relax when an electron is added or removed. This
relaxation will change the nodal structure of the guiding wavefunction.
The first set of DMC calculations were performed using the new
electron-electron interaction described in
section 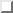 and a Slater determinant containing fixed
LDA orbitals. The value of the gap at the
and a Slater determinant containing fixed
LDA orbitals. The value of the gap at the 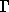 -point obtained
from adding and removing an electron under these conditions was
3.95
-point obtained
from adding and removing an electron under these conditions was
3.95  0.4 eV. This is almost within error bars of the
experimental gap of 3.4 eV.
0.4 eV. This is almost within error bars of the
experimental gap of 3.4 eV.
The same set of three calculations were repeated, but this time
allowing the LDA orbitals used in the Slater determinant to relax.
The value of the gap at the 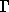 -point was reduced to
3.59
-point was reduced to
3.59  0.4 eV.
0.4 eV.
Finally, the calculations using the relaxed LDA orbitals were repeated
using the original Ewald expression for the electron-electron
interaction. The value of the gap at the 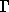 -point was
reduced further to 3.34
-point was
reduced further to 3.34  0.4 eV.
0.4 eV.
From these results it appears that
- The DMC performs at least as well, if not better than the VMC. This
is to be expected because the DMC calculations involving
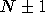 electrons do not suffer from the limitations in the one- and two-body
terms in the trial wavefunction.
electrons do not suffer from the limitations in the one- and two-body
terms in the trial wavefunction. - Relaxing the LDA orbitals used to construct the Slater
determinant appears to have a small beneficial effect on the DMC
results. This could be due to the relaxed orbitals reproducing the
nodal surface of the true many-body wavefunction more accurately than
fixed orbitals.
- There appears to be very little difference in DMC results for
gaps obtained using the new interaction described in
section
 and the original Ewald interaction. As
the new interaction is designed to remove the long range finite size
errors this suggests that the finite size errors present in the
gap are a short range effect not a long range effect as suggested in
Ref.[79]. The considerable finite size errors present in the
individual N, N+1 and N-1 calculations performed with the Ewald
interaction almost entirely cancel from the gap.
and the original Ewald interaction. As
the new interaction is designed to remove the long range finite size
errors this suggests that the finite size errors present in the
gap are a short range effect not a long range effect as suggested in
Ref.[79]. The considerable finite size errors present in the
individual N, N+1 and N-1 calculations performed with the Ewald
interaction almost entirely cancel from the gap.
The relative insensitivity of the gap energy to the choice of
electron-electron interaction is confirmed by the HF results. These
show a small but consistent improvement when using the new interaction
in preference to the Ewald interaction. For example in an n=2
system, the gap at the 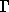 point is improved by 15% when using
the new interaction.
point is improved by 15% when using
the new interaction.



Next: Promoting Electrons
Up: Addition and Subtraction of
Previous: Addition and Subtraction of
Andrew Williamson
Tue Nov 19 17:11:34 GMT 1996
![]() -point as a test for comparing the DMC
with VMC and experiment. Two separate modifications to the DMC
algorithm were experimented with,
-point as a test for comparing the DMC
with VMC and experiment. Two separate modifications to the DMC
algorithm were experimented with,
![]() and a Slater determinant containing fixed
LDA orbitals. The value of the gap at the
and a Slater determinant containing fixed
LDA orbitals. The value of the gap at the ![]() -point obtained
from adding and removing an electron under these conditions was
3.95
-point obtained
from adding and removing an electron under these conditions was
3.95 ![]() 0.4 eV. This is almost within error bars of the
experimental gap of 3.4 eV.
0.4 eV. This is almost within error bars of the
experimental gap of 3.4 eV.
![]() -point was reduced to
3.59
-point was reduced to
3.59 ![]() 0.4 eV.
0.4 eV.
![]() -point was
reduced further to 3.34
-point was
reduced further to 3.34 ![]() 0.4 eV.
0.4 eV.
![]() point is improved by 15% when using
the new interaction.
point is improved by 15% when using
the new interaction.