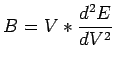 |
(1) |
In our bulk Silicon calculation we had a rigid supercell shape and the starting atomic positions of the silicon atoms
were those known to be correct. What effect will a variable cell calculation have?
In the cell file
FIX_ALL_CELL : FALSE
In the .param file our keywords are;
finite_basis_corr : 2
which ensures that an automatic finite basis set correction is made
The complete output is in the link. We see that the first three steps are indeed
singlepoint energy calculations
Calculating finite basis set correction with 3 cut-off energies.
Calculating total energy with cut-off of 270.000eV.
------------------------------------------------------------------------ <-- SCF
SCF loop Energy Energy gain Timer <-- SCF
per atom (sec) <-- SCF
------------------------------------------------------------------------ <-- SCF
Initial 0.00000000E+000 4.05 <-- SCF
1 -2.07999179E+002 1.03999590E+002 15.06 <-- SCF
2 -2.16644967E+002 4.32289377E+000 25.37 <-- SCF
3 -2.16547612E+002 -4.86773393E-002 35.44 <-- SCF
4 -2.16472419E+002 -3.75966977E-002 45.52 <-- SCF
5 -2.16473346E+002 4.63609274E-004 51.23 <-- SCF
6 -2.16473342E+002 -2.09197016E-006 55.58 <-- SCF
7 -2.16473343E+002 7.21451053E-007 59.95 <-- SCF
8 -2.16473343E+002 1.95459391E-008 64.28 <-- SCF
------------------------------------------------------------------------ <-- SCF
Final energy = -216.4733431455 eV (not corrected for finite basis set)
Calculating total energy with cut-off of 275.000eV.
------------------------------------------------------------------------ <-- SCF
SCF loop Energy Energy gain Timer <-- SCF
per atom (sec) <-- SCF
------------------------------------------------------------------------ <-- SCF
Initial -2.16473343E+002 65.79 <-- SCF
1 -2.16474422E+002 5.39545221E-004 72.46 <-- SCF
2 -2.16474423E+002 2.77186149E-007 76.73 <-- SCF
3 -2.16474423E+002 2.10512829E-007 81.13 <-- SCF
------------------------------------------------------------------------ <-- SCF
Final energy = -216.4744232114 eV (not corrected for finite basis set)
Calculating total energy with cut-off of 280.000eV.
------------------------------------------------------------------------ <-- SCF
SCF loop Energy Energy gain Timer <-- SCF
per atom (sec) <-- SCF
------------------------------------------------------------------------ <-- SCF
Initial -2.16474423E+002 82.48 <-- SCF
1 -2.16475528E+002 5.52276233E-004 89.09 <-- SCF
2 -2.16475528E+002 3.59413754E-007 93.47 <-- SCF
3 -2.16475529E+002 2.76001709E-007 97.85 <-- SCF
------------------------------------------------------------------------ <-- SCF
Final energy = -216.4755290347 eV (not corrected for finite basis set)
For future reference: finite basis dEtot/dlog(Ecut) = -0.061086eV
Total energy corrected for finite basis set = -216.475512 eV
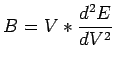 |
(1) |