Topology
Materials with topological electrons and phonons
Topology has emerged as a new tool to classify and understand phases of matter. Materials with nontrivial topology carry currents that cannot be stopped by impurities, exhibit electromagnetic effects beyond the standard Maxwell equations, and provide realisations of particles such as Weyl fermions that had so far only been theorised in particle physics. Potential applications are numerous, and one of the most exciting is the use of topology for the construction of robust quantum computers. From a theoretical point of view, the study of topological materials is interesting because it typically requires the use of quantum mechanics with the inclusion of relativistic effects.
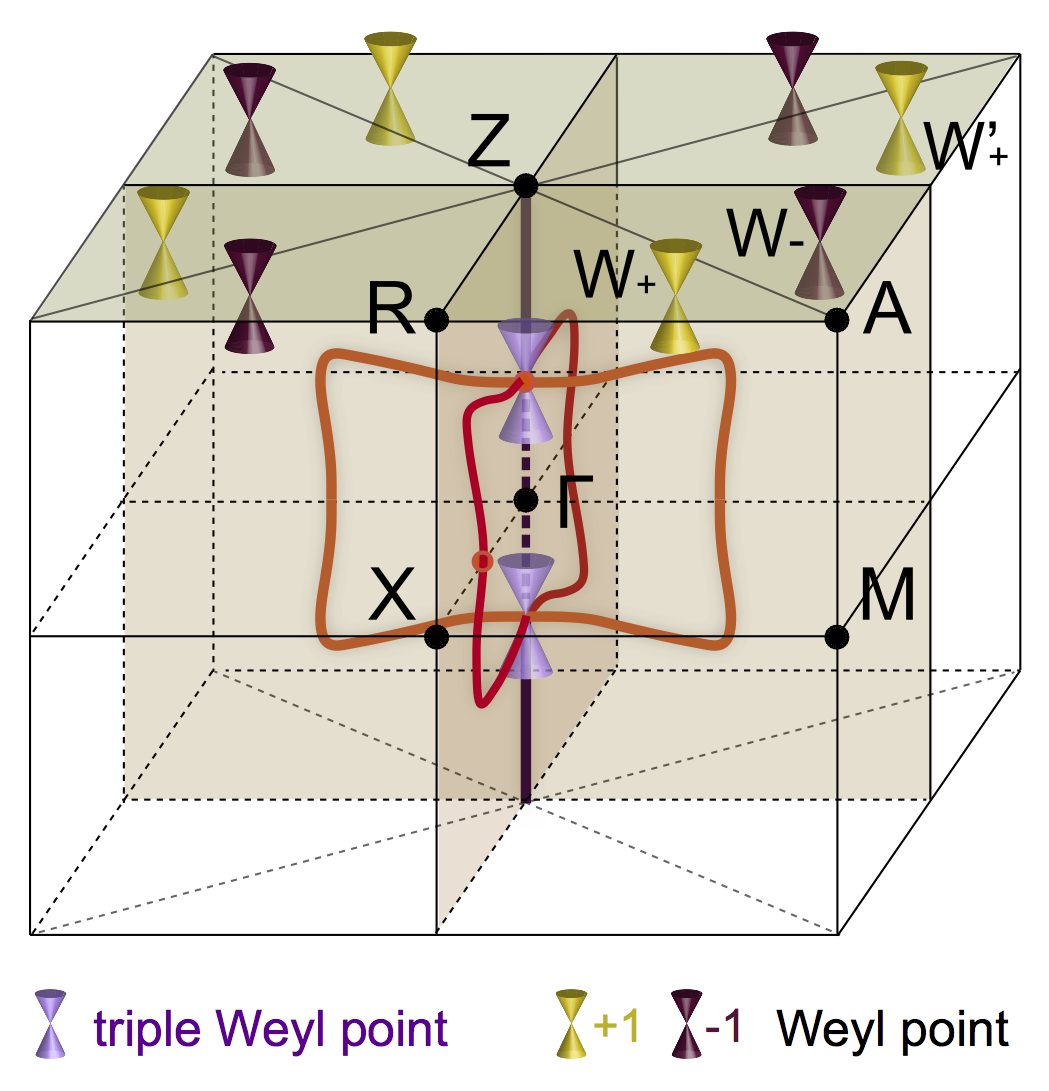
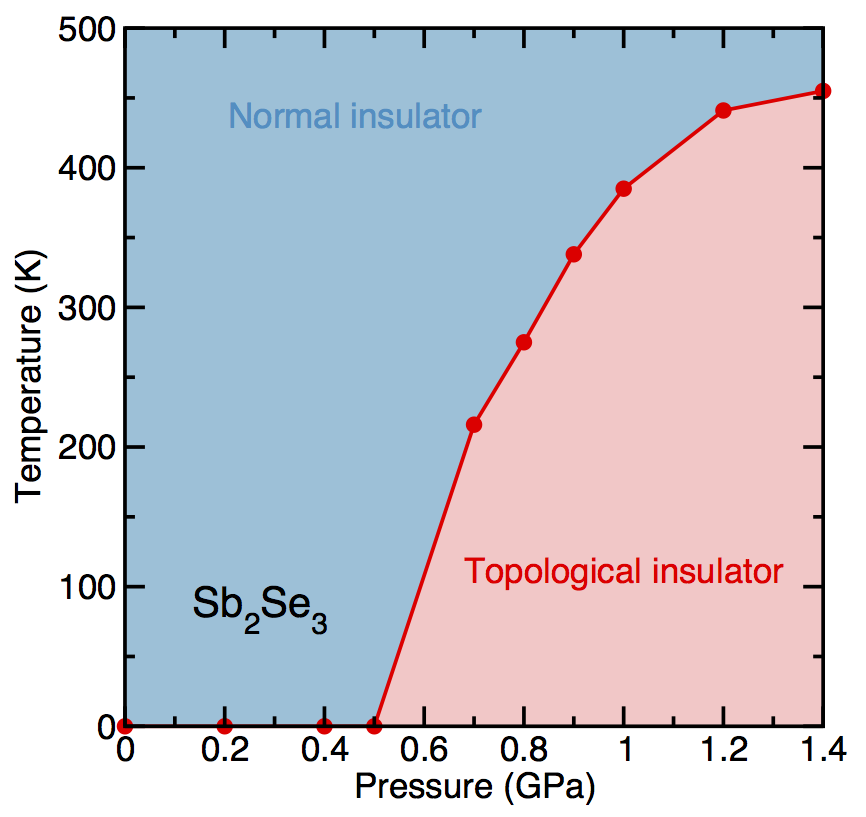
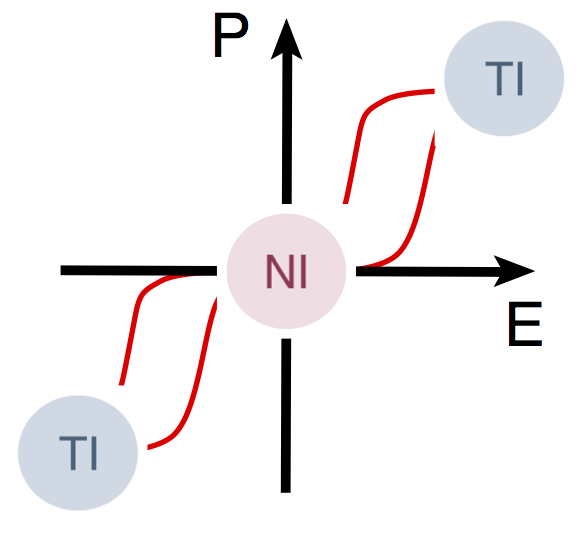
In our research, we investigate the microscopic properties of topological materials. As an example, we have studied how temperature can induce phase transitions between trivial and topological insulators via the coupling of electrons to lattice vibrations [ Physical Review Letters ], demonstrating how to design materials with topological effects that persist up to room temperature, a necessary condition for technological applications. This work has been highlighted in a Synopsis in Physics: Topological insulators feel the heat. Another example is the proposal of a new type of functional material, which we call an antiferroelectric topological insulator, in which an electric field can be used to control the topological order [ Physical Review Letters ]. A final example is the study of the topological properties of phonons (rather than electrons), which we have recently found to be ubiquitous in oxide perovskites [ Science Advances ].