Self-consistent electronic minimization

CASTEP offers a choice of methods for electronic relaxation. The default method is the most efficient and is based on density mixing (Kresse and Furthmuller, 1996). In this scheme, the sum of electronic eigenvalues is minimized in the fixed potential instead of the self-consistent minimization of the total energy. The new charge density at the end of the minimization is mixed with the initial density and the process is repeated until convergence is reached. A number of options are supported for this scheme: linear mixing, Kerker mixing, Broyden mixing, and Pulay mixing, in order of increasing robustness. The conjugate gradient-based approach is used to minimize the sum of eigenvalues. A slightly more elaborate scheme that involves separate mixing of spin density has been developed for spin-polarized calculations.

CASTEP also supports a more traditional scheme for electronic relaxation, involving minimization of the total energy. The electronic wavefunctions are expanded using a plane-wave basis set and the expansion coefficients are varied so as to minimize the total energy. This minimization is performed by using an all-bands method that allows simultaneous update of all wavefunctions. The scheme uses a preconditioned conjugate gradients technique (Payne et al., 1992).

The main advantage of the density mixing method is its robustness for metallic systems, especially for metallic surfaces. A traditional total energy minimization scheme might become unstable in a metallic system with the cell elongated in one dimension, which is the typical setup for supercell calculations on surfaces. The density mixing scheme converges equally well for insulating and metallic cases, and offers at least a factor of three increase in speed for moderately sized insulator systems.

When using the density mixing method, the SCF energy no longer decreases monotonically to the final converged SCF energy and unconverged energies may have values lower than the final converged energy. This behavior is due to the fact that in the density mixing method, the Harris functional for the energy is used, rather than the Kohn-Sham functional. Unlike the Kohn-Sham functional, the Harris functional does not necessarily have a minimum at the SCF solution.

Preconditioning

All electronic relaxation methods in CASTEP use preconditioning to speed up the rate of convergence (Payne et al., 1992). The idea is to find a matrix which, when multiplied with the residual vector, gives the exact error in the wavefunction. Formally, this matrix can be written down as:

Eq. CASTEP 28

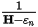
where ε_n is the exact eigenvalue for the band being optimized. It in not possible to evaluate this matrix, but by recognizing that the kinetic energy dominates the Hamiltonian for large G-vectors, it is possible to approximate the matrix by a diagonal function which converges to G^-2 for large G-vectors and is constant for small G-vectors. The actual form of the matrix is (Payne et al., 1992):

Eq. CASTEP 29

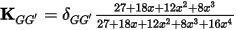
where x is the ratio of |k + G|² to the kinetic energy of the given state.

Application of the preconditioning scheme causes all of the large wave-vector components of a wavefunction to converge at nearly the same rate.

Density mixing schemes

CASTEP supports four schemes for generating new starting charge densities from the results of the previous SCF step (Kresse and Furthmuller, 1996). The simplest is the linear mixing scheme. This method requires one parameter and the output density is produced as a linear combination of the input and output densities on the last iteration.

Kerker mixing recognizes the fact that small-G components of the charge density should be mixed with smaller weights in order to prevent charge sloshing during SCF optimization. The new density is given by:

Eq. CASTEP 30

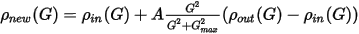
The Kerker scheme is, consequently, defined by two parameters, the mixing amplitude, A, and the cutoff wavevector, G_max.

The most efficient mixing scheme is Pulay's scheme. In this approach, the input charge density and the residual vectors are stored over a number of SCF optimization steps. A new input density is obtained in each step as a linear combination of charge densities of all previous steps. The new density is determined such that it minimizes the normal of the residual vector subject to the constraint of conserving the number of electrons. Pulay's scheme starts with a Kerker-type step, so it is effectively controlled by three parameters: the mixing amplitude, A, the cutoff wavevector, G_max, and the depth of the optimization history.

Broyden mixing is very similar to the Pulay scheme, except that it performs a quasi-Newton relaxation instead of DIIS minimization of the residuals.

Treatment of metallic systems

The main difference between metals and insulators, from the technical point of view, is that the number of occupied bands is not the same at different k-points in the Brillouin zone. The number of occupied bands for insulators is calculated as one half the total number of valence electrons, but this approach is not suitable for metals. Partial occupancies are introduced to eliminate discontinuous changes in total energy that are created when an energy band crosses a Fermi level during SCF minimization.

The overall strategy for treating metallic systems in CASTEP is as follows. The number of bands has to be slightly higher than would be required for an insulator. It may be necessary to add more bands if convergence is slow, especially for spin-polarized systems. An artificial electronic temperature is then introduced by assuming Gaussian-like smearing of each energy level (de Vita, 1992). Occupation numbers are deduced from the ratio of the area of the Gaussian that falls below the Fermi level to its total area. Thus, a level deep in the valence band has an occupation number of 1, a level directly on the Fermi surface has an occupation number of 0.5, and a level high above the Fermi energy is empty. In some sense, this is the same as giving the Kohn-Sham particles a finite temperature. Therefore, CASTEP uses the Mermin finite temperature expression for the total energy (Marzari, 1997):

E = E_KS - TS

where:

T is the temperature (that is, smearing width)
S is the Mermin entropy due to the different ways in which the partially filled bands could have been filled

The CASTEP output is as follows. The line

Final energy, E = -861.8315373731 eV

gives the Kohn-Sham energy, E_KS, which ignores the entropy. However, it is the total Mermin free energy that is minimized by CASTEP and reported in the SCF cycles in the line

Final free energy (E-TS) = -861.8315374521 eV

If you were actually interested in the electronic states at some reasonable nonzero temperature, you would smear the Fermi level with a thermal (that is, Fermi-Dirac) smearing method and the free energy reported by CASTEP would be the value you require.

Temperature equivalent of energy is given by the conversion factor of 11604.5 K/eV; so the default smearing width of 0.1 eV corresponds to a very high temperature of 1160 K.

However, it is often the T = 0 K value that is required and the smearing is necessary to improve the convergence of the numerical algorithm. As the smearing ('temperature') is increased, the TS term increases and the free energy, E_KS - TS, goes down. At the same time, as the entropy contributes more and more to the free energy, the electronic minimization pays less attention to theE_KS term, so the final E_KS increases. Because the dependence of the free energy and the Kohn-Sham energy on the smearing width is the same (to first order), averaging the two values gives a much better approximation to the T = 0 K result:

NB est. 0K energy (E-0.5TS) = -861.8315374126 eV

The total energy calculated by CASTEP for metals is thereby corrected for the fact that it now includes the artificial electronic entropy contribution. This correction is possible because a closed analytical form for the dependence of the total energy on the smearing width (or electronic temperature), s, exists. In principle, evaluation of E_tot (s -> 0) is necessary in order to obtain a physically meaningful energy. In the past, values for s as low as 0.01 eV have been used to calculate the converged energy. The total energy correction described above allows the use of a much higher smearing width (up to 1 eV), while still giving results converged with respect to s. The advantage is the added stability of the calculation, since occasional Fermi-level crossings do not create instabilities. However, there is no simple expression for a similar correction for either atomic forces or stress on the unit cell.

The error in the forces introduced by this limitation is generally small and acceptable. Nonetheless, geometry optimizations for metals should be performed with some caution. You should use smaller smearing values than for single-point energy runs. The calculated forces will be more accurate, but there is a risk of instability, since changes in atomic geometry are likely to cause reordering of bands and some Fermi-level crossings. Cell optimization is also more difficult for metallic systems, since the stress tensor could be affected by nonphysical contributions from nearly empty conduction bands.