



Next: Conjugate gradients
Up: thesis
Previous: Further work
Contents
Bessel function identities
A. . Bessel function identities
In this appendix we list some standard results used in the analysis
of chapter 5 [186].
| |
|
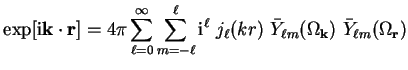 |
(A.1) |
| |
|
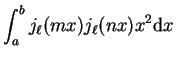 |
(A.2) |
| |
|
![$\displaystyle \exp[{\mathrm{i}} {\bf k} \cdot {\bf r}] = 4 \pi
\sum_{\ell=0}^{\...
...\ell}(k r)~{\bar Y}_{\ell m} (\Omega_{\bf k})~{\bar Y}_{\ell m}(\Omega_{\bf r})$](img1229.gif) |
(A.3) |
| |
|
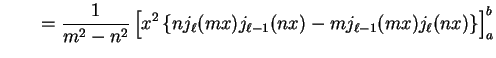 |
|
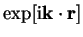 |
|
![$\displaystyle \qquad
= \frac{1}{m^2 - n^2} \left[ x^2 \left\{ n j_{\ell}(m x) j_{\ell-1}(n
x) - m j_{\ell-1}(m x) j_{\ell}(n x) \right\} \right]_{a}^{b}$](img1231.gif) |
(A.4) |
| |
|
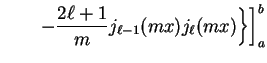 |
|
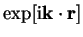 |
|
![$\displaystyle \biggl. \biggl. \qquad - {2\ell + 1
\over m} j_{\ell - 1} (m x) j_{\ell} (m x) \biggr\} \biggr]_{a}^{b}$](img1233.gif) |
(A.5) |
Peter D. Haynes
1999-09-21
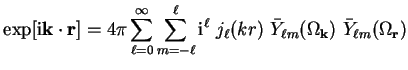
![$\displaystyle \exp[{\mathrm{i}} {\bf k} \cdot {\bf r}] = 4 \pi
\sum_{\ell=0}^{\...
...\ell}(k r)~{\bar Y}_{\ell m} (\Omega_{\bf k})~{\bar Y}_{\ell m}(\Omega_{\bf r})$](img1229.gif)
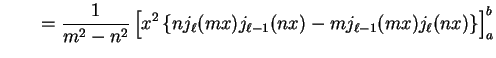
![$\displaystyle \qquad
= \frac{1}{m^2 - n^2} \left[ x^2 \left\{ n j_{\ell}(m x) j_{\ell-1}(n
x) - m j_{\ell-1}(m x) j_{\ell}(n x) \right\} \right]_{a}^{b}$](img1231.gif)
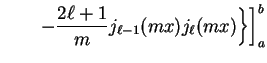
![$\displaystyle \biggl. \biggl. \qquad - {2\ell + 1
\over m} j_{\ell - 1} (m x) j_{\ell} (m x) \biggr\} \biggr]_{a}^{b}$](img1233.gif)