Paper abstract

Keywords: computer-simulation, electronic-structure calculations, ab-initio calculations, embedded-cluster, density-functional theory

INTRODUCTION

The power of ab initio calculations has increased rapidly in recent years. In this paper we start by reviewing the present capability of first-principles calculations and point out some of the limitations of present conventional techniques. We then focus on linear-scaling techniques and discuss the extent to which they do represent a significant step forward in first-principles approaches. We review hybrid modelling schemes which also provide a route to much larger system-sizes and explain why linear-scaling approaches are the method of choice for the first-principles element of such schemes. Finally we briefly describe our work on the development of an ab initio linear-scaling code based upon a penalty-functional method.

CONVENTIONAL TECHNIQUES

The speed of progress in first-principles calculations over the fifteen years since Car and Parrinello's introduction of a unified scheme for density-functional theory (DFT) and molecular dynamics [1] has been breathtaking. The combination of the universal adoption of density-functional theory [2], significant improvements in numerical methods [3] and the availability of powerful computers has allowed first-principles studies of systems containing as many as a thousand atoms from the whole periodic table, typically yielding predictions of physical and chemical properties with an accuracy of a few percent. A critical aspect of calculations on systems of this size and complexity is the optimisation of atomic positions, since experiment is not capable of providing this information to sufficient accuracy. It is even possible to perform dynamical simulations in which the forces on the atoms are calculated from first principles and to study quantum effects in the ionic system using Feynman's path integral formulation [4].

While the power of modern first-principles calculations is impressive, it is important to appreciate that accessible system-sizes and time-scales are actually very limited: a system containing a thousand atoms typically has a volume of only 20 cubic angstroms. Although structural optimisation is possible in most first-principles codes, in general the true minimum energy ionic configuration will only be found if the connectivity of the ionic system is correctly specified. While dynamical simulations are in principle possible in any first-principles scheme that calculates ionic forces, in practice only the total energy pseudopotential technique has successfully used dynamics to address real scientific questions.

LINEAR-SCALING TECHNIQUES

The computational cost of conventional wavefunction-based total energy schemes scales at least as the cube of the number of atoms in the system. Many linear-scaling first-principles schemes have been proposed over the years [5,6,7,8]. While these schemes will allow calculations for very large numbers of atoms, there are other technical problems that may prevent the extraction of useful scientific information from such calculations. In particular, the length-scales and, more importantly, time-scales are still extremely limited. A system containing a million atoms is still only 200 cubic angstroms in volume, and the relevant time-scales (or equivalently the complexity of the phase space) increase very rapidly with system-size. Furthermore, in such a large simulation most of the atoms will be very close to their bulk configuration and, even using a linear-scaling algorithm, considerable computational effort will be expended describing regions of the system where a full first-principles calculation is not required.

HYBRID MODELLING SCHEMES

A schematic illustration of a hybrid modelling scheme applied to a block of materials containing two cracks is shown in Fig. 1. Ab initio techniques are applied in the lightest shaded regions containing the crack tip, where accurate quantum-mechanical description of the bond-breaking process is essential. In the surrounding region, empirical interatomic potentials are used, and in the darkest shaded region continuum modelling is used. This approach allows each region of a system to be described by the modelling technique best-suited to the accuracy required in each region and also addresses the problem of multiple length-scales.

Fig. 1: schematic illustration of a hybrid modelling scheme.

PENALTY-FUNCTIONAL METHOD

The cubic scaling of traditional ab initio methods arises in general either from the cost of diagonalizing the Hamiltonian or from orthogonalizing the wavefunctions in iterative schemes. Most linear-scaling techniques have been developed by reformulating the quantum-mechanical equations in terms of generalized Wannier functions or the single-particle density-matrix, instead of the extended single-particle wavefunctions. Enforcing the localization of the Wannier functions or truncating the density-matrix beyond a certain range results in a linear-scaling method. However, although many such schemes have been proposed [5,6,7,8], progress towards a truly general purpose scheme has been rather slow. Some of the problems encountered in implementing linear-scaling schemes are the existence of multiple minima in the energy surface, and slow convergence towards the electronic ground-state, even when the correct minimum is located. The result is a method with a computational cost that is linear in the number of atoms but with a very large prefactor so that the linear-scaling calculation only becomes faster than conventional schemes for extremely large systems.

In order to address the problems mentioned above, we are attempting to formulate a linear-scaling scheme with the following features:

• Single minimum in the search space.
• Fast, guaranteed convergence to this minimum from any starting configuration.
• Computational cost and memory as small as possible making the technique competitive with conventional techniques even for moderately sized systems.

As mentioned above, the cubic scaling of conventional techniques results from the cost of solving Schrödinger's equation for the single-particle wavefunctions which are the eigenfunctions of the Kohn-Sham Hamiltonian. Within a self-consistent ab initio scheme it is also necessary to find the ground-state electronic density, but since this stage of the calculation already scales linearly with system-size, we will only address the solution of Schrödinger's equation for a fixed electronic density (and thus Hamiltonian). In a conventional scheme this may be achieved by diagonalizing the Hamiltonian (directly or iteratively) in the representation of some set of basis functions. Plane-waves and Gaussians have been popular choices for this purpose. We have chosen to use truncated spherical-waves [11] for this purpose for the following reasons:

• Truncated spherical-waves naturally obey the boundary conditions imposed to truncate the density-matrix (or localize the Wannier functions).
• The completeness of the basis set may be controlled by means of a kinetic energy cut-off, as for plane-waves.
• Meaningful comparison may thus be made to the results of plane-wave calculations.
• Quantities such as the overlap matrix and matrix elements of the kinetic energy and non-local pseudopotential operators may be calculated analytically.

Instead of solving for the extended wavefunctions, we choose to solve for the single-particle density-matrix which contains the same information but is not subject to the constraint of orthogonality and is short-ranged so that it may be truncated yielding a linear-scaling technique. In conventional methods, the lowest energy wavefunctions are occupied according to Pauli's exclusion principle, but in density-matrix-based schemes, the occupation numbers of these wavefunctions become variable parameters and it is necessary to impose the following constraints:

• Normalization: the occupation numbers must sum to the correct number of electrons in the system.
• Idempotency: the occupation numbers should be zero or unity, in order to obey the Pauli exclusion principle.

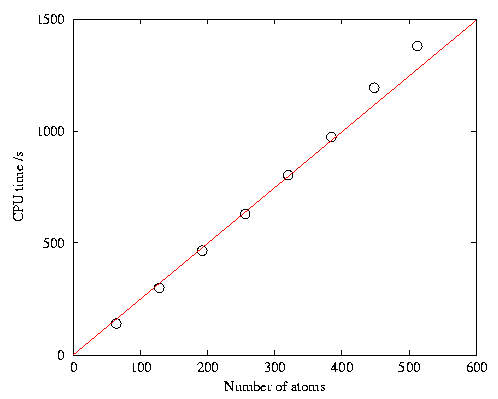
Fig. 2: scaling of the penalty-functional method with system-size.

In conclusion, we have shown that although linear-scaling techniques are a significant step forward in the development of ab initio quantum-mechanical calculations with respect to the range of applications to which such methods may be applied, they do not in themselves overcome all of the limitations of conventional techniques. We have argued that the combination of ab initio linear-scaling techniques with hybrid modelling schemes is essential in order to efficiently and accurately model large-scale processes in real materials which are of interest to scientists and engineers today. We have outlined some of our work towards achieving this goal, namely the development of a penalty-functional-based ab initio linear-scaling scheme.

REFERENCES

1. R. Car and M. Parrinello, "Unified Approach for Molecular Dynamics and Density-Functional Theory", Phys. Rev. Lett. 55, 2471 (1985).
   
2. P. Hohenberg and W. Kohn, "Inhomogeneous Electron Gas", Phys. Rev. 136, 864 (1964);
   W. Kohn and L. J. Sham, "Self-Consistent Equations Including Exchange and Correlation Effects", ibid. 140, 1133 (1965);
   for a review see, for instance, R. O. Jones and O. Gunnarsson, "The density functional formalism, its applications and prospects", Rev. Mod. Phys. 61, 689 (1989).
   
3. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, "Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients", Rev. Mod. Phys. 64, 1045 (1992).
   
4. See, for instance, M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids pp. 270ff. (Oxford University Press, 1987).
   
5. W. Yang, "Direct Calculation of Electron Density in Density-Functional Theory", Phys. Rev. Lett. 66, 1438 (1991);
   W. Yang and T.-S. Lee, "A density-matrix divide-and-conquer approach for electronic structure calculations of large molecules", J. Chem. Phys. 103, 5674 (1995);
   S. Baroni and P. Giannozzi, "Towards Very Large-Scale Electronic-Structure Calculations", Europhys. Lett. 17, 547 (1992);
   D. A. Drabold and O. F. Sankey, "Maximum Entropy Approach for Linear Scaling in the Electronic Structure Problem", Phys. Rev. Lett. 70, 3631 (1993);
   L.-W. Wang, "Calculating the density of states and optical-absorption spectra of large quantum systems by the plane-wave moments method", Phys. Rev. B 49, 10154 (1994);
   O. F. Sankey, D. A. Drabold and A. Gibson, "Projected random vectors and the recursion method in the electronic-structure problem", ibid. 50, 1376 (1994);
   R. N. Silver and H. Röder, "Calculation of the densities of states and spectral functions by Chebyshev recursion and maximum entropy", Phys. Rev. E 56, 4822 (1997);
   S.-Y. Qiu, C. Z. Wang, K. M. Ho and C. T. Chan, "Tight-binding molecular dynamics with linear system-size scaling", J. Phys.: Condens. Matter 6, 9153 (1994);
   A. Canning, G. Galli, F. Mauri, A. de Vita and R. Car, "O(N) tight-binding molecular dynamics on massively parallel computers: an orbital decomposition approach", Comp. Phys. Comm. 94, 89 (1996);
   A. P. Horsfield, A. M. Bratkovsky, D. G. Pettifor and M. Aoki, "Bond-order potential and cluster recursion for the description of chemical-bonds -- efficient real-space methods for tight-binding molecular-dynamics", Phys. Rev. B 53, 1656 (1996);
   Y. Wang et al., "Order-N Multiple Scattering Approach to Electronic Structure Calculations", Phys. Rev. Lett. 75, 2867 (1995);
   I. A. Abrikosov et al., "Order-N Green's Function Technique for Local Environment Effects in Alloys", Phys. Rev. Lett. 76, 4203 (1996);
   I. A. Abrikosov et al., "Locally self-consistent Green's function approach to the electronic structure problem", Phys. Rev. B 56, 9319 (1997);
   E. Smargiassi and P. A. Madden, "Orbital-free kinetic-energy functionals for first-principles molecular dynamics", ibid. 49, 5220 (1994);
   M. Foley and P. A. Madden, "Further orbital-free kinetic-energy functionals for ab initio molecular dynamics", ibid. 53, 10589 (1996);
   S. Goedecker and L. Colombo, "Efficient Linear Scaling Algorithm for Tight-Binding Molecular Dynamics", Phys. Rev. Lett. 73, 122 (1994);
   S. Goedecker and M. Teter, "Tight-binding electronic-structure calculations and tight-binding molecular dynamics with localized orbitals", Phys. Rev. B 51, 9455 (1995);
   R. Baer and M. Head-Gordon, "Chebyshev expansion methods for electronic structure calculations on large molecular systems", J. Chem. Phys. 107, 10003 (1997);
   U. Stephan and D. A. Drabold, "Order-N projection method for first-principles computations of electronic quantities and Wannier functions", Phys. Rev. B 57, 6391 (1998);
   D. M. C. Nicholson and X.-G. Zhang, "Approximate occupation functions for density-functional calculations", ibid. 56, 12805 (1997);
   F. Gagel, "Finite-Temperature Evaluation of the Fermi Density Operator", J. Comp. Phys. 139, 399 (1998);
   R. N. Silver, H. Röder, A. F. Voter and J. D. Kress, "Kernel Polynomial Approximations for Densities of States and Spectral Functions", ibid. 124, 115 (1996);
   A. F. Voter, J. D. Kress and R. N. Silver, "Linear-scaling tight binding from a truncated approach", Phys. Rev. B 53, 12733 (1996);
   G. Galli and M. Parrinello, "Large Scale Electronic Structure Calculations", Phys. Rev. Lett. 69, 3547 (1992);
   F. Mauri, G. Galli and R. Car, "Orbital formulation for electronic-structure calculations with linear system-size scaling", Phys. Rev. B 47, 9973 (1993);
   F. Mauri and G. Galli, "Electronic-structure calculations and molecular-dynamics simulations with linear system-size scaling", ibid. 50, 4316 (1994);
   P. Ordejón, D. A. Drabold, M. P. Grumbach and R. M. Martin, "Unconstrained minimization approach for electronic computations that scales linearly with system size", ibid. 48, 14646 (1993);
   P. Ordejón, D. A. Drabold, R. M. Martin and M. P. Grumbach, "Linear system-size scaling methods for electronic-structure calculations", ibid. 51, 1456 (1995);
   J. Kim, F. Mauri and G. Galli, "Total-energy global optimizations using nonorthogonal localized orbitals", ibid. 52, 1640 (1995);
   K. C. Pandey, A. R. Williams and J. F. Janak, "Localized orbital theory of electronic structure: A simple application", ibid. 52, 14415 (1995);
   P. Ordejón, E. Artacho and J. M. Soler, "Self-consistent order-{$N$} density-functional calculations for very large systems", ibid. 53, 10441 (1996);
   for reviews see, for instance, D. R. Bowler et al., "A comparison of linear scaling tight-binding methods", Modelling Simul. Mater. Sci. Eng. 5, 199 (1997);
   G. Galli, "Linear scaling methods for electronic structure calculations and quantum molecular dynamics simulations", Current Opinion in Solid State and Materials Science 1, 864 (1996).
   
6. X.-P. Li, R. W. Nunes and D. Vanderbilt, "Density-matrix electronic-structure method with linear system-size scaling", Phys. Rev. B 47, 10891 (1993);
   M. S. Daw, "Model for energetics of solids based on the density matrix", ibid. 47, 10895 (1993);
   E. B. Stechel, A. R. Williams and P. J. Feibelman, "N-scaling algorithm for density-functional calculations of metals and insulators", ibid. 49, 10088 (1994);
   W. Hierse and E. B. Stechel, "Order-N methods in self-consistent density-functional calculations", ibid. 50, 17811 (1994);
   E. Hernández and M. J. Gillan, "Self-consistent first-principles technique with linear scaling", ibid. 51, 10157 (1995);
   E. Hernández, M. J. Gillan and C. M. Goringe, "Linear-scaling density-functional-theory technique: The density-matrix approach", ibid. 53, 7147 (1996).
   
7. W. Kohn, "Density Functional and Density Matrix Method Scaling Linearly with the Number of Atoms", Phys. Rev. Lett. 76, 3168 (1996).
   
8. P. D. Haynes and M. C. Payne, "Corrected penalty-functional method for linear-scaling calculations within density-functional theory", Phys. Rev. B 59, 12173 (1999).
   
9. V. B. Shenoy, R. Miller, E. B. Tadmor, R. Phillips and M. Ortiz, "Quasicontinuum models of interfacial structure and deformation", Phys. Rev. Lett. 80, 742 (1998);>br> R. Miller, E. B. Tadmor, R. Phillips and M. Ortiz, "Quasicontinuum simulation of fracture at the atomic scale", Modelling Simul. Mater. Sci. Eng. 6, 607 (1998);
   V. B. Shenoy, R. Miller, E. B. Tadmor, D. Rodney, R. Phillips and M. Ortiz, "An adaptive finite element approach to atomic-scale mechanics - the quasicontinuum method", J. Mech. Phys. Solids 47, 611 (1999);
   E. B. Tadmor, G. S. Smith, N. Bernstein and E. Kaxiras, "Mixed finite element and atomistic formulation for complex crystals", Phys. Rev. B 59, 235 (1999);
   F. F. Abraham, J. Q. Broughton, N. Bernstein and E. Kaxiras, "Spanning the continuum to quantum length scale in a dynamic simulation of brittle fracture", Europhys. Lett. 44, 783 (1998);
   R. E. Rudd and J. Q. Broughton, "Coarse-grained molecular dynamics and the atomic limit of finite elements", Phys. Rev. B 58, 5893 (1998).
   
10. U. Eichler, C. M. Kolmel and J. Sauer, "Combining ab initio techniques with analytical potential functions for structure predictions of large systems: Method and application to crystalline silica polymorphs", J. Comput. Chem. 18, 463 (1997);
    U. Eichler, M. Brandle and J. Sauer, "Predicting absolute and site specific acidities for zeolite catalysts by a combined quantum mechanics interatomic potential function approach", J. Phys. Chem. B 101, 10035 (1997);
    M. Brandle, J. Sauer, R. Dovesi and N. M. Harrison, "Comparison of a combined quantum mechanics/interatomic potential function approach with its periodic quantum-mechanical limit: Proton siting and ammonia adsorption in zeolite chabazite", J. Chem. Phys. 109, 10379 (1998);
    M. Brandle and J. Sauer, "Acidity differences between inorganic solids induced by their framework structure. A combined quantum mechanics molecular mechanics ab initio study on zeolites", J. Am. Chem. Soc. 120, 1556 (1998);
    M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, "ONIOM: A multilayered integrated MO+MM method for geometry optimizations and single point energy predictions. A test for Diels-Alder reactions and Pt(P(t-Bu)(3))(2)+H-2 oxidative addition", J. Phys. Chem. 100, 19357 (1996);
    T. Matsubara, S. Sieber and K. Morokuma, "A test of the new 'integrated M0+MM' (IMOMM) method for the conformational energy of ethane and n-butane", Int. J. Quantum Chem. 60, 1101 (1996);
    R. D. J. Froese, D. G. Musaev and K. Morokuma, "Theoretical study of substituent effects in the diimine-M(II) catalyzed ethylene polymerization reaction using the IMOMM method", J. Am. Chem. Soc. 120, 1581 (1998).
    
11. P. D. Haynes and M. C. Payne, "Localised spherical-wave basis set for O(N) total-energy pseudopotential calculations", Comp. Phys. Comm. 102, 17 (1997).
    
12. R. McWeeny, "Some Recent Advances in Density Matrix Theory", Rev. Mod. Phys. 32, 335 (1960).
    
13. S. Goedecker, "Linear Scaling Electronic Strcuture Methods", to appear in Rev. Mod. Phys. (1999).
    
14. P. D. Haynes and M. C. Payne, "Failure of density-matrix minimization methods for linear-scaling density-functional theory using the Kohn penalty functional", Solid State Communications 108, 737 (1998).
    

ACKNOWLEDGMENTS

This work was supported by grant GR/L55346 from the Engineering and Physical Sciences Research Council, UK.

Paper abstract