

Next: Bibliography Up: Paper abstract
Corrected penalty-functional method for linear-scaling
calculations within density-functional theory
P. D. Haynes and M. C. Payne
Theory of Condensed Matter, Cavendish Laboratory,
Madingley Road, Cambridge CB3 0HE, United Kingdom
October 6, 1998
We present a new method for the calculation of ground-state total
energies within density-functional theory, based upon the
single-particle density-matrix formulation, which requires a
computational effort which scales only linearly with system-size. The
difficult idempotency constraint is imposed approximately using a
penalty-functional constructed to allow efficient minimization. The
resulting error in the total energy due to the violation of
idempotency is removed by an analytic correction. The results for a
system comprising 216 atoms of crystalline silicon are compared with
those from a standard plane-wave code. Linear scaling to 512 atoms is
also demonstrated on a workstation.
PACS numbers: 71.15.Mb
Within density-functional theory (DFT), the complexity of the
problem of calculating the ground-state energy of the inhomogeneous
electron gas in an external potential [1] scales
linearly with system-size 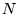 (i.e. the number of
electrons). However, `traditional' methods based upon the Kohn-Sham
(KS) formulation of DFT [2] require a computational
effort which scales asymptotically as
(i.e. the number of
electrons). However, `traditional' methods based upon the Kohn-Sham
(KS) formulation of DFT [2] require a computational
effort which scales asymptotically as 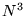 , either because of the
cost of diagonalizing the Hamiltonian, or as a result of the
orthogonality requirement for the extended KS single-particle
wave-functions.
This
, either because of the
cost of diagonalizing the Hamiltonian, or as a result of the
orthogonality requirement for the extended KS single-particle
wave-functions.
This 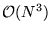 scaling restricts the size of systems which can
currently be treated. Much interest has therefore been shown in using
the single-particle density-matrix (DM) to calculate the total energy
[3]. Since the DM is short-ranged in real-space
[4] and free from orthogonality constraints, it
provides the basis of a linear-scaling method for KS-DFT
[5,6,7] (see
[8] for a review of some of these methods). However,
most linear-scaling schemes have so far been applied only in the
context of tight-binding or restricted basis-set calculations. In
contrast, the method presented here has been applied to fully
self-consistent DFT calculations with an arbitrarily complete
basis-set, a task so far attempted by only one other group
[6].
scaling restricts the size of systems which can
currently be treated. Much interest has therefore been shown in using
the single-particle density-matrix (DM) to calculate the total energy
[3]. Since the DM is short-ranged in real-space
[4] and free from orthogonality constraints, it
provides the basis of a linear-scaling method for KS-DFT
[5,6,7] (see
[8] for a review of some of these methods). However,
most linear-scaling schemes have so far been applied only in the
context of tight-binding or restricted basis-set calculations. In
contrast, the method presented here has been applied to fully
self-consistent DFT calculations with an arbitrarily complete
basis-set, a task so far attempted by only one other group
[6].
In terms of the KS wave-functions 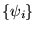 and occupancies
and occupancies
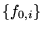 , the ground-state DM
, the ground-state DM
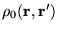 is
is
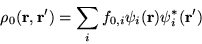 |
(1) |
where the occupancies equal zero or unity for wave-functions
with KS eigenvalues above or below the chemical potential
respectively. Defining the energy functional by
where
![$E_{\mathrm{Hxc}}[n]$](img17.png) is the sum of the Hartree and
exchange-correlation energies which depend only on the electronic
density
is the sum of the Hartree and
exchange-correlation energies which depend only on the electronic
density
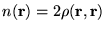 (the factor of two
arising from spin degeneracy), and
(the factor of two
arising from spin degeneracy), and
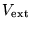 is the external
potential arising from the ions. The ground-state energy is found by
minimizing this functional with respect to all Hermitian DMs
satisfying
is the external
potential arising from the ions. The ground-state energy is found by
minimizing this functional with respect to all Hermitian DMs
satisfying
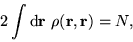 |
(3) |
and the idempotency condition
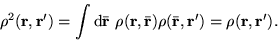 |
(4) |
This can be achieved in 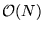 operations by exploiting the
short-ranged nature of the DM and truncating it beyond some spatial
cut-off
operations by exploiting the
short-ranged nature of the DM and truncating it beyond some spatial
cut-off
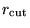 i.e. imposing
i.e. imposing
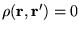 for
for
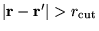 .
.
The idempotency condition is required to ensure that the
occupancies are all zero or unity. It is difficult to enforce
since it is a non-linear constraint. One approach has been to use a
purifying transformation [9] to drive the DM
towards idempotency during minimization
[3,6]. The approach most closely related to
that introduced in this work is due to Kohn who, in a recent Letter
[10], added a penalty-functional to the KS energy
functional so that the minimum value of the total functional is
achieved for the idempotent ground-state DM 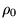 . In terms of a
trial Hermitian DM
. In terms of a
trial Hermitian DM 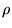 and its eigenvalues
and its eigenvalues 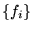 , Kohn's
penalty-functional is
, Kohn's
penalty-functional is
![\begin{displaymath}
P[\rho] = \left\{ \int {\mathrm d}{\bf r} \left[ \rho^2
(1 -...
...over 2}
= \left[ \sum_i f_i^2 (1 - f_i)^2 \right]^{1 \over 2}.
\end{displaymath}](img29.png) |
(5) |
The square-root is required to force the total functional to take its
minimum value at the ground-state, because the energy is not
variational with respect to changes in the occupancies. However, the
branch point introduced means that the gradient is undefined at the
ground-state and the functional cannot be minimized using standard
techniques such as the conjugate gradients algorithm, since
information from local gradients cannot be used to build up a picture
of the global behaviour of the total functional [12].
In this Letter, we introduce a generalized functional ![$Q[\rho]$](img30.png) defined by
defined by
![\begin{displaymath}
Q[\rho] = E[\rho] + \alpha P^2[\rho] .
\end{displaymath}](img31.png) |
(6) |
The Taylor series for this functional in terms of the occupancies is
well-defined at all points, so that it may be minimized
efficiently. Although the total functional 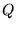 may possess multiple
minima for certain values of
may possess multiple
minima for certain values of 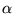 , there is only one minimum where
the normalization constraint (3) is also satisfied
[11], and since the search over trial DMs may be
straightforwardly constrained to normalized DMs, multiple minima do
not cause problems in practice.
, there is only one minimum where
the normalization constraint (3) is also satisfied
[11], and since the search over trial DMs may be
straightforwardly constrained to normalized DMs, multiple minima do
not cause problems in practice.
Although the penalty-functional 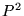 will prevent `run-away'
solutions (such as macroscopic occupation of the low-energy bands at
the expense of negatively filling higher bands) so that the
minimization process is stable (which is not guaranteed by other
schemes), the DM
will prevent `run-away'
solutions (such as macroscopic occupation of the low-energy bands at
the expense of negatively filling higher bands) so that the
minimization process is stable (which is not guaranteed by other
schemes), the DM 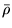 which minimizes the functional will not
be exactly idempotent. In general, the occupancies
which minimizes the functional will not
be exactly idempotent. In general, the occupancies
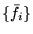 corresponding to occupied bands will exceed unity, and those
corresponding to unoccupied bands will be negative. We estimate the
errors in the occupancies
corresponding to occupied bands will exceed unity, and those
corresponding to unoccupied bands will be negative. We estimate the
errors in the occupancies
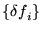 defined by
defined by
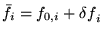 in the following manner: since the
functional
in the following manner: since the
functional 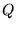 is minimized by
is minimized by 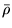 , it is a minimum with
respect to all changes in the occupancies which maintain the
normalization constraint (3), imposed by introducing a
Lagrange multiplier
, it is a minimum with
respect to all changes in the occupancies which maintain the
normalization constraint (3), imposed by introducing a
Lagrange multiplier 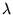 :
:
![\begin{displaymath}
\frac{\partial}{\partial f_i} \left\{ Q[\rho] - \lambda \lef...
...{\bf r},{\bf r}) - N \right] \right\}_{f_i = {\bar
f}_i} = 0 .
\end{displaymath}](img39.png) |
(7) |
Using Janak's theorem [13] for the derivative of the
energy functional 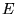 in terms of the KS eigenvalues
in terms of the KS eigenvalues
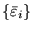 at the minimum of the functional, we obtain:
at the minimum of the functional, we obtain:
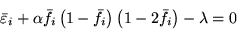 |
(8) |
so assuming that the
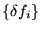 are small,
are small,
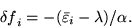 |
(9) |
Application of the normalization constraint (3) requires
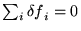 from which
from which
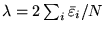 is obtained.
The variance of the occupancy errors is related to the
variance of the energy eigenvalues, scaled by the parameter
is obtained.
The variance of the occupancy errors is related to the
variance of the energy eigenvalues, scaled by the parameter 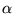 .
As
.
As 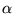 is increased, the errors in the eigenvalues at the minimum
decrease as
is increased, the errors in the eigenvalues at the minimum
decrease as
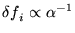 . For small deviations
from idempotency, the penalty-functional
. For small deviations
from idempotency, the penalty-functional
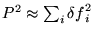 so that the penalty term
so that the penalty term 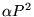 also decreases as
also decreases as
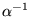 , and the energy approaches the true ground-state
energy. This behaviour is illustrated in Fig. 1 where the
occupancy errors are plotted for four bands as a function of
, and the energy approaches the true ground-state
energy. This behaviour is illustrated in Fig. 1 where the
occupancy errors are plotted for four bands as a function of
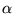 .
.
Figure 1:
Variation of occupancy errors with 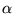 . Dotted
lines show the best fit to
. Dotted
lines show the best fit to 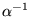 behaviour.
behaviour.
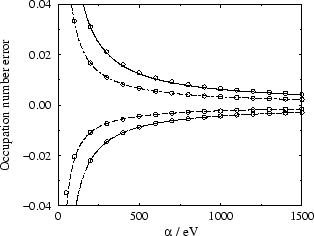 |
This 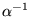 convergence is unsatisfactory for practical
applications, since it requires large values of
convergence is unsatisfactory for practical
applications, since it requires large values of 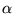 to obtain
accurate estimates of the ground-state energy and at large values of
to obtain
accurate estimates of the ground-state energy and at large values of
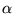 the penalty term dominates the total functional and hinders
efficient minimization of the energy term. To overcome this problem we
present a method for obtaining accurate values for the ground-state
energy from the results of calculations performed at much smaller
values of
the penalty term dominates the total functional and hinders
efficient minimization of the energy term. To overcome this problem we
present a method for obtaining accurate values for the ground-state
energy from the results of calculations performed at much smaller
values of 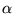 .
At the minimum of the total functional,
.
At the minimum of the total functional,
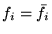 ,
,
![\begin{displaymath}
\left. \frac{\partial Q[\rho]}{\partial f_i} \right\vert _{{...
...i}
+ 2 \alpha {\bar f}_i (1 - {\bar f}_i) (1 - 2 {\bar f}_i) .
\end{displaymath}](img52.png) |
(10) |
This expression can be used to construct a first-order Taylor
expansion for the total energy with respect to the occupancies. We can
provide an estimate for the ground-state energy 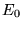 as
as
![\begin{displaymath}
E_0 = E[\rho_0] \approx E[{\bar \rho}] + 2 \alpha \sum_i {\bar f}_i (1
- {\bar f}_i) (1 - 2 {\bar f}_i) {\delta f}_i .
\end{displaymath}](img54.png) |
(11) |
For occupied bands,
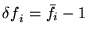 whereas for
unoccupied bands
whereas for
unoccupied bands
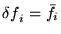 so that
so that
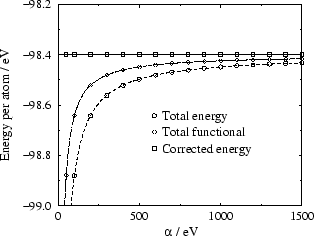
Figure 2:
Variation of the total energy, total functional and corrected
energy with 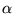 . Dotted lines show the best fit to
. Dotted lines show the best fit to 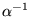 behaviour.
behaviour.
 |
The first term of the correction has been written as a sum over all
bands so that it can be expressed in terms of a trace
![${\rm Tr}[{\bar
\rho} (1 - \bar \rho)^2 (1 - 2 {\bar \rho})]$](img63.png) , which can always be
evaluated in
, which can always be
evaluated in 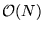 operations. The second term only
contributes when unoccupied bands are included in the calculation,
which is not necessary for insulators. A single eigenvalue of the
(sparse) DM can always be obtained in
operations. The second term only
contributes when unoccupied bands are included in the calculation,
which is not necessary for insulators. A single eigenvalue of the
(sparse) DM can always be obtained in 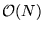 operations and so
it is possible to evaluate the correction for a small number of
unoccupied bands without spoiling the
operations and so
it is possible to evaluate the correction for a small number of
unoccupied bands without spoiling the 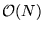 scaling. Even so,
since the correction is only applied when the minimum of the total
functional has been found, a single
scaling. Even so,
since the correction is only applied when the minimum of the total
functional has been found, a single 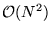 step to obtain all
of the eigenvalues of the DM is still an insignificant fraction of the
total computational effort. Importantly, this analytic correction also
permits the calculation of forces consistent with the corrected
energy. However, the electronic density and Kohn-Sham eigenvalues
calculated by the method remain in error, although the former is
qualitatively correct and thus still useful for visualization.
Fig. 2 shows the total energy, the total functional and the
corrected energy as a function of
step to obtain all
of the eigenvalues of the DM is still an insignificant fraction of the
total computational effort. Importantly, this analytic correction also
permits the calculation of forces consistent with the corrected
energy. However, the electronic density and Kohn-Sham eigenvalues
calculated by the method remain in error, although the former is
qualitatively correct and thus still useful for visualization.
Fig. 2 shows the total energy, the total functional and the
corrected energy as a function of 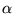 . Even at
. Even at 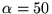 eV,
the corrected energy agrees with the
eV,
the corrected energy agrees with the
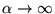 limits of both the total energy and total functional to better than
limits of both the total energy and total functional to better than
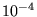 eV per atom.
eV per atom.
The lowest-order term omitted from the Taylor expansion involves
the second derivative
![\begin{displaymath}
{1 \over 2} \left. \frac{\partial^2 E[\rho]}{\partial f_i \p...
... \varepsilon}_i}{\partial f_j} \right\vert _{f_j = {\bar f}_j}
\end{displaymath}](img68.png) |
(13) |
which is known as the chemical hardness matrix in the context of the
construction of transferable pseudopotentials [14]. This
matrix is neither positive- nor negative-definite, so that the
corrected energy is neither an upper nor a lower bound to the true
ground-state energy. However, this error is much smaller than those
arising from the finite DM cut-off, so that in practice the corrected
energy can be treated as a variational upper bound to the ground-state
energy.
In practical 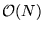 calculations, we cannot work directly
with the extended KS wave-functions and occupancies, and
instead the trial DM is written in terms of a sparse matrix
calculations, we cannot work directly
with the extended KS wave-functions and occupancies, and
instead the trial DM is written in terms of a sparse matrix 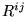 and a set of non-orthogonal functions
and a set of non-orthogonal functions 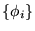 localized within
spherical regions of radius
localized within
spherical regions of radius
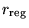 :
:
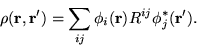 |
(14) |
The sparsity of 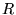 is controlled by the parameter
is controlled by the parameter 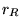 , forcing
elements of
, forcing
elements of 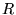 corresponding to localized functions with centres
separated by more than
corresponding to localized functions with centres
separated by more than 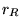 to vanish.
to vanish.
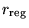 and
and 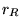 together determine
together determine
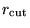 . The
localized functions are expanded in some localized basis, and then the
total functional is minimized with respect to the expansion
coefficients and the matrix elements
. The
localized functions are expanded in some localized basis, and then the
total functional is minimized with respect to the expansion
coefficients and the matrix elements 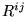 .
.
The minimization is performed by two nested loops, the inner with
respect to 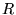 and the outer with respect to the
and the outer with respect to the 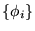 . In
terms of the Hamiltonian in the representation of the
. In
terms of the Hamiltonian in the representation of the 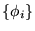 ,
,
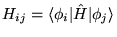 and the overlap
matrix
and the overlap
matrix
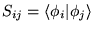 , the gradient with
respect to
, the gradient with
respect to 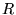 is
is
![\begin{displaymath}
\frac{\partial Q[\rho]}{\partial R^{ij}} =
2 H_{ji} + 2 \alpha \left[ SRS(1-RS)(1-2RS) \right]_{ji} .
\end{displaymath}](img75.png) |
(15) |
In contrast to other orbital-based methods, the condition number for
this stage of the minimization is approximately unity (since the
curvature of the functional with respect to variations of 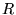 is
determined by the shape of
is
determined by the shape of 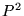 alone) and hence the minimization is
much more efficient [15]. By making the Löwdin
transformation to a set of orthonormalized orbitals
alone) and hence the minimization is
much more efficient [15]. By making the Löwdin
transformation to a set of orthonormalized orbitals
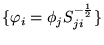 and defining the DM and
Hamiltonian in this representation as
and defining the DM and
Hamiltonian in this representation as
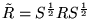 and
and
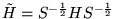 respectively, then at the constrained minimum defined by
(7);
respectively, then at the constrained minimum defined by
(7);
![\begin{displaymath}
2 S^{1 \over 2} \left[ {\tilde H} + \alpha {\tilde R}(1 - {\tilde R})
(1 - 2 {\tilde R}) - \lambda \right] S^{1 \over 2} = 0
\end{displaymath}](img79.png) |
(16) |
i.e.
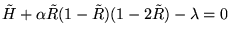 so that the DM and the Hamiltonian
commute and can therefore be diagonalized simultaneously. (In terms of
this representation (14),
so that the DM and the Hamiltonian
commute and can therefore be diagonalized simultaneously. (In terms of
this representation (14),
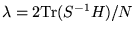 , although its value is never required). The resulting eigenvalues
obey (8).
, although its value is never required). The resulting eigenvalues
obey (8).
The gradient with respect to the localized functions is
When transformed to the common diagonal frame of the DM
and Hamiltonian by some unitary transformation
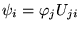 , this gradient becomes
, this gradient becomes
![\begin{displaymath}
\frac{\delta Q}{\delta \psi_i^{\ast}({\bf r})} = 2 f_i \left[ {\hat H}
+ \alpha f_i (1-f_i)(1-2f_i) \right] \psi_i({\bf r}) .
\end{displaymath}](img86.png) |
(18) |
At the minimum of 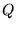 with respect to both
with respect to both 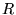 and
and 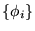 we
thus have from (8):
we
thus have from (8):
These are simply the Kohn-Sham equations, with eigenvalues shifted by
the Lagrange multiplier 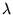 associated with the normalization
constraint. Thus, in addition to kinetic-energy preconditioning
[16], occupancy preconditioning [17] can
be applied to improve the convergence.
associated with the normalization
constraint. Thus, in addition to kinetic-energy preconditioning
[16], occupancy preconditioning [17] can
be applied to improve the convergence.
This scheme has been implemented and applied to the test case of
216 atoms of crystalline silicon. The localized functions were
expanded in a spherical-wave basis-set [18] using an
energy cut-off of 200 eV and angular momentum components up to 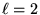 . In Fig. 3 the convergence of the corrected energy with
respect to
. In Fig. 3 the convergence of the corrected energy with
respect to
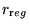 and
and 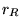 is plotted. As these spatial
cut-offs are increased, the variational freedom of the DM is
increased, so that the energy converges from above.
is plotted. As these spatial
cut-offs are increased, the variational freedom of the DM is
increased, so that the energy converges from above.
Figure 3:
Convergence of the corrected energy with respect to (left)
the localization region radius
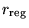 and (right) the
cut-off
and (right) the
cut-off 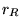 applied to the matrix
applied to the matrix 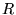 .
.
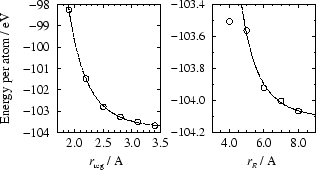 |
Table 1 shows values for the equilibrium lattice
parameter 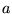 and bulk modulus
and bulk modulus 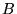 obtained using values of
obtained using values of
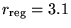 Å,
Å, 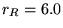 Å and
Å and 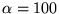 eV.
Experimental values and results of the CASTEP plane-wave code
[19], using the same pseudopotential
[20] and equivalent Brillouin zone sampling are also
shown. The calculations of
eV.
Experimental values and results of the CASTEP plane-wave code
[19], using the same pseudopotential
[20] and equivalent Brillouin zone sampling are also
shown. The calculations of 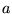 agree to better than 1% and those of
agree to better than 1% and those of
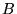 (which is more sensitive to the data) to within 3%.
(which is more sensitive to the data) to within 3%.
Table 1:
Comparison of calculated and experimental data for
crystalline silicon.
| Calculation |
Linear-scaling |
CASTEP |
Experiment |
|
|
|
|
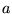 / Å / Å |
5.428 |
5.390 |
5.430 |
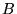 / GPa / GPa |
104.3 |
101.7 |
100.0 |
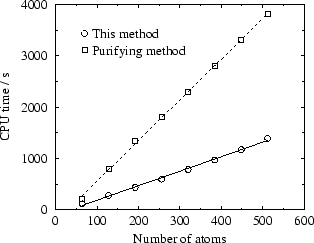
Finally, in Fig. 4 the computational effort for a
single iteration of the outer loop for the same values of
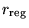 ,
, 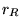 and
and 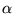 is plotted against system-size
to demonstrate the linear scaling of the method. Since fewer matrix
multiplications are required, each iteration of this method is cheaper
than the purifying method, also plotted (both methods require a
similar number of iterations to converge the energy to a given
accuracy). The number of iterations required to converge these
linear-scaling calculations is currently an order of magnitude larger
(about 200 for these calculations on silicon) than is the case for
traditional cubic-scaling all-bands methods [21], but
since the condition number of the functional depends only upon
properties of the system being modelled, the number of iterations
required does not increase with system-size. Since the method
achieves linear scaling by partitioning real-space into overlapping
regions, excellent scaling with respect to the number of processors is
expected for implementations on massively-parallel computers
[22].
is plotted against system-size
to demonstrate the linear scaling of the method. Since fewer matrix
multiplications are required, each iteration of this method is cheaper
than the purifying method, also plotted (both methods require a
similar number of iterations to converge the energy to a given
accuracy). The number of iterations required to converge these
linear-scaling calculations is currently an order of magnitude larger
(about 200 for these calculations on silicon) than is the case for
traditional cubic-scaling all-bands methods [21], but
since the condition number of the functional depends only upon
properties of the system being modelled, the number of iterations
required does not increase with system-size. Since the method
achieves linear scaling by partitioning real-space into overlapping
regions, excellent scaling with respect to the number of processors is
expected for implementations on massively-parallel computers
[22].
Figure 4:
Scaling of computational effort with system-size for this
method compared with a method based on the purifying transformation
(DEC 500au workstation).
 |
In conclusion, we have presented a new DM-based linear-scaling
method for DFT, in which the approximate imposition of idempotency,
enforced by means of a penalty-functional, permits the use of
efficient minimization methods, and from which accurate estimates of
the energy derived from the true idempotent ground-state DM can be
obtained by using a correction derived from the form of the
penalty-functional.
We acknowledge useful discussions with I. D. White, and PDH
acknowledges the support of an EPSRC studentship. This work is covered
by British Patent Application No. 9814931.3.



Next: Bibliography
Peter D. Haynes
2002-10-25
![]() (i.e. the number of
electrons). However, `traditional' methods based upon the Kohn-Sham
(KS) formulation of DFT [2] require a computational
effort which scales asymptotically as
(i.e. the number of
electrons). However, `traditional' methods based upon the Kohn-Sham
(KS) formulation of DFT [2] require a computational
effort which scales asymptotically as ![]() , either because of the
cost of diagonalizing the Hamiltonian, or as a result of the
orthogonality requirement for the extended KS single-particle
wave-functions.
This
, either because of the
cost of diagonalizing the Hamiltonian, or as a result of the
orthogonality requirement for the extended KS single-particle
wave-functions.
This ![]() scaling restricts the size of systems which can
currently be treated. Much interest has therefore been shown in using
the single-particle density-matrix (DM) to calculate the total energy
[3]. Since the DM is short-ranged in real-space
[4] and free from orthogonality constraints, it
provides the basis of a linear-scaling method for KS-DFT
[5,6,7] (see
[8] for a review of some of these methods). However,
most linear-scaling schemes have so far been applied only in the
context of tight-binding or restricted basis-set calculations. In
contrast, the method presented here has been applied to fully
self-consistent DFT calculations with an arbitrarily complete
basis-set, a task so far attempted by only one other group
[6].
scaling restricts the size of systems which can
currently be treated. Much interest has therefore been shown in using
the single-particle density-matrix (DM) to calculate the total energy
[3]. Since the DM is short-ranged in real-space
[4] and free from orthogonality constraints, it
provides the basis of a linear-scaling method for KS-DFT
[5,6,7] (see
[8] for a review of some of these methods). However,
most linear-scaling schemes have so far been applied only in the
context of tight-binding or restricted basis-set calculations. In
contrast, the method presented here has been applied to fully
self-consistent DFT calculations with an arbitrarily complete
basis-set, a task so far attempted by only one other group
[6].
![]() and occupancies
and occupancies
![]() , the ground-state DM
, the ground-state DM
![]() is
is
![$\displaystyle - \int {\mathrm d}{\bf r}' \left[ \nabla_{\bf r}^2
\rho({\bf r},{\bf r}') \right]_{{\bf r}={\bf r}'} + E_{\mathrm{Hxc}}[n]$](img15.png)
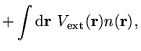
![]() . In terms of a
trial Hermitian DM
. In terms of a
trial Hermitian DM ![]() and its eigenvalues
and its eigenvalues ![]() , Kohn's
penalty-functional is
, Kohn's
penalty-functional is
![\begin{displaymath}
P[\rho] = \left\{ \int {\mathrm d}{\bf r} \left[ \rho^2
(1 -...
...over 2}
= \left[ \sum_i f_i^2 (1 - f_i)^2 \right]^{1 \over 2}.
\end{displaymath}](img29.png)
![]() defined by
defined by
![]() will prevent `run-away'
solutions (such as macroscopic occupation of the low-energy bands at
the expense of negatively filling higher bands) so that the
minimization process is stable (which is not guaranteed by other
schemes), the DM
will prevent `run-away'
solutions (such as macroscopic occupation of the low-energy bands at
the expense of negatively filling higher bands) so that the
minimization process is stable (which is not guaranteed by other
schemes), the DM ![]() which minimizes the functional will not
be exactly idempotent. In general, the occupancies
which minimizes the functional will not
be exactly idempotent. In general, the occupancies
![]() corresponding to occupied bands will exceed unity, and those
corresponding to unoccupied bands will be negative. We estimate the
errors in the occupancies
corresponding to occupied bands will exceed unity, and those
corresponding to unoccupied bands will be negative. We estimate the
errors in the occupancies
![]() defined by
defined by
![]() in the following manner: since the
functional
in the following manner: since the
functional ![]() is minimized by
is minimized by ![]() , it is a minimum with
respect to all changes in the occupancies which maintain the
normalization constraint (3), imposed by introducing a
Lagrange multiplier
, it is a minimum with
respect to all changes in the occupancies which maintain the
normalization constraint (3), imposed by introducing a
Lagrange multiplier ![]() :
:
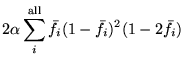
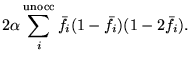

![\begin{displaymath}
{1 \over 2} \left. \frac{\partial^2 E[\rho]}{\partial f_i \p...
... \varepsilon}_i}{\partial f_j} \right\vert _{f_j = {\bar f}_j}
\end{displaymath}](img68.png)
![]() calculations, we cannot work directly
with the extended KS wave-functions and occupancies, and
instead the trial DM is written in terms of a sparse matrix
calculations, we cannot work directly
with the extended KS wave-functions and occupancies, and
instead the trial DM is written in terms of a sparse matrix ![]() and a set of non-orthogonal functions
and a set of non-orthogonal functions ![]() localized within
spherical regions of radius
localized within
spherical regions of radius
![]() :
:
![]() and the outer with respect to the
and the outer with respect to the ![]() . In
terms of the Hamiltonian in the representation of the
. In
terms of the Hamiltonian in the representation of the ![]() ,
,
![]() and the overlap
matrix
and the overlap
matrix
![]() , the gradient with
respect to
, the gradient with
respect to ![]() is
is
![$\displaystyle \frac{\delta Q[\rho]}{\delta \phi_i^{\ast}({\bf r})}$](img82.png)
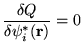
![]() . In Fig. 3 the convergence of the corrected energy with
respect to
. In Fig. 3 the convergence of the corrected energy with
respect to
![]() and
and ![]() is plotted. As these spatial
cut-offs are increased, the variational freedom of the DM is
increased, so that the energy converges from above.
is plotted. As these spatial
cut-offs are increased, the variational freedom of the DM is
increased, so that the energy converges from above.

![]() and bulk modulus
and bulk modulus ![]() obtained using values of
obtained using values of
![]() Å,
Å, ![]() Å and
Å and ![]() eV.
Experimental values and results of the CASTEP plane-wave code
[19], using the same pseudopotential
[20] and equivalent Brillouin zone sampling are also
shown. The calculations of
eV.
Experimental values and results of the CASTEP plane-wave code
[19], using the same pseudopotential
[20] and equivalent Brillouin zone sampling are also
shown. The calculations of ![]() agree to better than 1% and those of
agree to better than 1% and those of
![]() (which is more sensitive to the data) to within 3%.
(which is more sensitive to the data) to within 3%.
![]() ,
, ![]() and
and ![]() is plotted against system-size
to demonstrate the linear scaling of the method. Since fewer matrix
multiplications are required, each iteration of this method is cheaper
than the purifying method, also plotted (both methods require a
similar number of iterations to converge the energy to a given
accuracy). The number of iterations required to converge these
linear-scaling calculations is currently an order of magnitude larger
(about 200 for these calculations on silicon) than is the case for
traditional cubic-scaling all-bands methods [21], but
since the condition number of the functional depends only upon
properties of the system being modelled, the number of iterations
required does not increase with system-size. Since the method
achieves linear scaling by partitioning real-space into overlapping
regions, excellent scaling with respect to the number of processors is
expected for implementations on massively-parallel computers
[22].
is plotted against system-size
to demonstrate the linear scaling of the method. Since fewer matrix
multiplications are required, each iteration of this method is cheaper
than the purifying method, also plotted (both methods require a
similar number of iterations to converge the energy to a given
accuracy). The number of iterations required to converge these
linear-scaling calculations is currently an order of magnitude larger
(about 200 for these calculations on silicon) than is the case for
traditional cubic-scaling all-bands methods [21], but
since the condition number of the functional depends only upon
properties of the system being modelled, the number of iterations
required does not increase with system-size. Since the method
achieves linear scaling by partitioning real-space into overlapping
regions, excellent scaling with respect to the number of processors is
expected for implementations on massively-parallel computers
[22].
