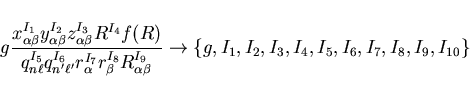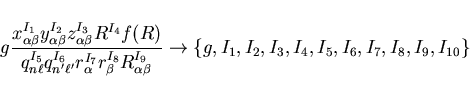

Next: 8. Conclusions
Up: Localised spherical-wave basis set
Previous: 6. Non-local pseudopotential
The results in equations
(19,20,22,
23) have been
written in a form which shows that in general each term can be
represented by a real numerical prefactor, integers which are the
powers of
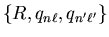 and one further integer
to signify the presence of one of the terms
and one further integer
to signify the presence of one of the terms
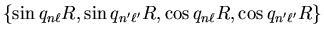 . When these terms are combined and differentiated by the
. When these terms are combined and differentiated by the
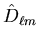 , the general term also needs integers to represent powers
of
, the general term also needs integers to represent powers
of
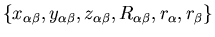 . Therefore a general term in the
expressions for
. Therefore a general term in the
expressions for
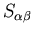 and
and
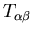 could be
represented by a data structure consisting of one real variable
could be
represented by a data structure consisting of one real variable 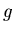 and ten integer variables
and ten integer variables 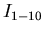 as follows:
as follows:
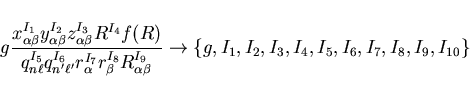 |
(36) |
with the following correspondence between 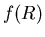 and
and 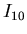 :
:
A recursive function can be written to manipulate these encoded terms
and perform the differentiation by the
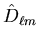 , which can
themselves be generated using the recursion rules for the associated
Legendre polynomials. Thus it is straightforward to write a code which
starts from equation (14) and generates the results up to
arbitrary values of
, which can
themselves be generated using the recursion rules for the associated
Legendre polynomials. Thus it is straightforward to write a code which
starts from equation (14) and generates the results up to
arbitrary values of 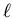 for
for
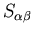 and
and
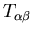 for the cases when
for the cases when
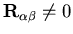 . The
results for
. The
results for
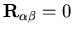 are simple enough to be coded
within the program which uses this basis.
are simple enough to be coded
within the program which uses this basis.
We have successfully implemented this basis set in a total-energy
pseudopotential code and are currently performing preliminary
calculations. For a given ionic configuration the matrix elements
between the basis states can be calculated initially and stored on
disk for use during the calculation.


Next: 8. Conclusions
Up: Localised spherical-wave basis set
Previous: 6. Non-local pseudopotential
Peter Haynes