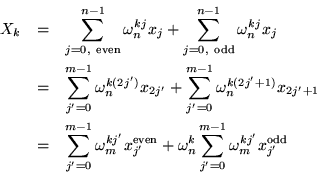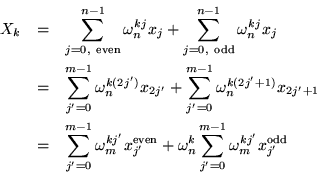

Next: Fast Fourier Transforms
Up: Contents
Previous: Slow Fourier Transforms
G. C. Danielson and C. Lanczos, ``Some improvements in
practical Fourier analysis and their application to X-ray scattering
from liquids'', J. Franklin Inst. 233, 365 (1942).
For even 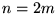 :
:
since
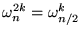 and writing
and writing
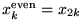 and
and
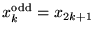 .
.
Peter D. Haynes
2001-11-07