Nonlinear Dynamics of Ferromagnets
A ferromagnetic material contains many interacting magnetic moments
that,
in the groundstate, line up to point in the same direction everywhere
within
the sample (or within each magnetic domain). If the ferromagnet is
excited
energetically, disturbing the magnetic moments away from this
mutually-parallel
conformation, their directions in space will undergo some temporal
dynamics
or oscillation before eventually relaxing through dissipation.
Understanding this dynamics poses a difficult problem: there
is a large number of coupled degrees of freedom, which
evolve according to a non-linear dynamics. Furthermore, any
description is complicated
by topological constraints involving the global conformation of
magnetic
moments. I am interested in studying the non-linear dynamics of
ferromagnets
(including insulating, itinerant, and ``quantum Hall'' ferromagnets),
and
understanding the properties of highly-excited ferromagnets, such as
itinerant
ferromagnets or quantum Hall ferromagnets under conditions of
high
current density.
Surprisingly, it turns out that insulating ferromagnetic
materials support excitations that are closely analogous to the vortex
rings of fluid dynamics
(familiar to us all as ``smoke-rings''). These are spatially-localized
non-linear disturbances that propagate without change of shape at a
constant
velocity through the ferromagnet (compare the ideal motion of a
circular
smoke ring, which moves at constant velocity through the air without
change
of radius). In fact, for reasons related to topology,
there
exists a sequence of magnetic vortex ring solitary waves that
are
classified by a topological invariant known as the Hopf invariant. (Two
configurations corresponding to different values of the Hopf
topological
invariant cannot be interconverted by smooth deformations.)
The images below illustrate typical conformations of the two
simplest
magnetic vortex ring excitations: with Hopf invariant equal to zero and
one (this difference in the global topology of the two configurations
can
be deduced from the different linking properties of the red and green
curves).
The direction of propagation of each excitation is perpendicular to the
plane containing the red circle.
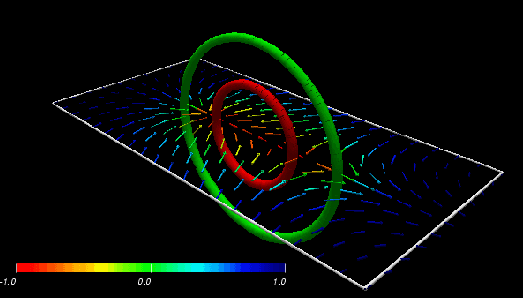
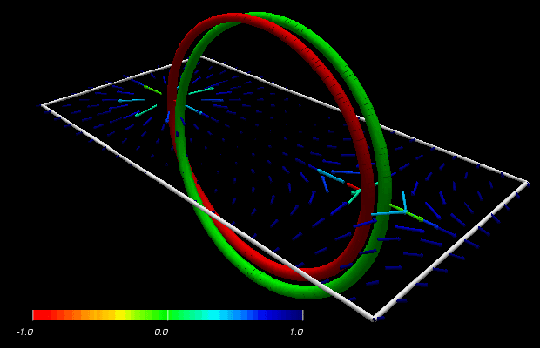
The images show the orientations of the magnetic
moments
within a plane cutting through the centre of the magnetic vortex ring.
The vectors represent the orientation of the local magnetic
moment
projected onto the x-y plane, while their colours indicate the z
component
of the magnetic moment (see colour legend). The red and green curves
indicate
the loci of points in space where the magnetic moment points in the -z
direction and the +x direction, respectively.
Publications
Propagating Magnetic Vortex Rings in Ferromagnets
N. R. Cooper
Phys. Rev. Lett. 82, 1554 (1999). [PRL,
cond-mat/9901037]
Solitary Waves in Planar Ferromagnets and the Breakdown of the
Spin-Polarized
Quantum Hall Effect
N. R. Cooper
Phys. Rev. Lett. 80, 4554 (1998). [PRL,
cond-mat/9801160]