The order is not important. This is all classical physics, so all the fields are just numbers which commute with each other (in quantum mechanics, the fields become operators and do not necessarily commute with each other).
Yes, the definition of N(ω) should be taken as given. This was not derived here. As mentioned in lectures, for relativistic systems it is the natural (Lorentz invariant) phase space density.
You need to compute the E-L equation ∂ν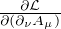 =
= 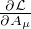 . Indeed, the
derivative
. Indeed, the
derivative 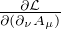 appears in (4.48) (up to replacing the labels on indices).
However, now there is the ∂ν acting on it, which means that the term
ends up rather different from those in (4.48). NB you need also to use the
Lorenz gauge condition.
appears in (4.48) (up to replacing the labels on indices).
However, now there is the ∂ν acting on it, which means that the term
ends up rather different from those in (4.48). NB you need also to use the
Lorenz gauge condition.
Indeed, the susceptibility is defined as the derivative at B = 0, hence the form of (7.38).
The equation in the middle of page 81 sets the Heaviside function Θ(t) to be 0 for t < 0 (NB limit of integral) and to be the limitϵ → 0 of e-ϵt for t > 0 (i.e. this is indistinguishable from 1 for any finite t and sufficiently small ϵ). So it is still the step function.
The identificiation is made in the time domain (it occurs within the
integral). It is put into a Fourier transform to generate the FT Θ(ω).
[Unhelpfully, the notes do not use a different symbol for the Heaviside
function, Θ(t), and its Fourier transform, Θ(ω), other than implicitly by
the change in argument. The FT is, of course, a different function, so
perhaps should better have been denoted 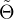 (ω).]
(ω).]
The first (real) part is a standard representation of the Dirac delta function. This should have been mentioned in the IB NatSci Maths course. It appears in equation (3.5b) of these notes. The second part may, similarly, be taken as a representation of the Cauchy principal part. This may well be new to those taking this course, but should be understood in a similar manner to the Dirac delta function. (i.e. you can view this limiting expression as a definition of what one means by the principal part P of the integral of 1∕ω, just as one can take the other limiting expression to be what you mean by the Dirac delta function inside an integral.)
Since the Schrödinger equation is first-order in time, for times t > t′
the wavefunction ψ(x,t) can be taken to be the solution of the equation
iℏ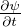 +
+ 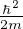 ∇2ψ = iℏδ(t - t′)ψ(x,t′) with the boundary condition that
ψ(t) = 0 for t < t′. [To see this: (i) note that for t > t′ the right hand side
is zero, so ψ(x,t) satisfies the time-dependent Schrödinger equation; (ii)
by integrating over an infinitesimal interval of time either side of t = t′,
one recovers the initial condition that ψ(x,t = t′) = ψ(t′).]
∇2ψ = iℏδ(t - t′)ψ(x,t′) with the boundary condition that
ψ(t) = 0 for t < t′. [To see this: (i) note that for t > t′ the right hand side
is zero, so ψ(x,t) satisfies the time-dependent Schrödinger equation; (ii)
by integrating over an infinitesimal interval of time either side of t = t′,
one recovers the initial condition that ψ(x,t = t′) = ψ(t′).]
However, this equation is equivalent to (8.12) with a “source” F(x,t) =
 ℏψ(x,t′)δ(t - t′). Putting this into (8.13), where the Green’s function
G is defined, and comparing with the definition of
ℏψ(x,t′)δ(t - t′). Putting this into (8.13), where the Green’s function
G is defined, and comparing with the definition of 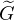 via ψ(x,t) =
∫
via ψ(x,t) =
∫
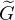 (x,t;x′,t′)ψ(x′,t′) dx′, shows that
(x,t;x′,t′)ψ(x′,t′) dx′, shows that 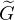 = iℏG.
= iℏG.
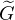 (x,t;x′,t′)ψ(x′,t′) dx′, How
can this integral be a funtion of x, t only? I think it
should be a function of x, t, and t’.
(x,t;x′,t′)ψ(x′,t′) dx′, How
can this integral be a funtion of x, t only? I think it
should be a function of x, t, and t’.
It is not necessarily a function of t′. The t′ dependences of 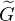 (x,t;x′,t′)
and ψ(x′,t′) cancel. For example, for a time-independent Hamiltonian, in
ket notation, we have
(x,t;x′,t′)
and ψ(x′,t′) cancel. For example, for a time-independent Hamiltonian, in
ket notation, we have
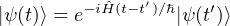
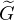 (x,t;x′,t′) = ⟨x|e-iĤ(t-t′)∕ℏ|x′⟩.
(x,t;x′,t′) = ⟨x|e-iĤ(t-t′)∕ℏ|x′⟩.
When there is a pole on the real axis, the integral along the real axis is not defined. We need to decide how to define it. The top diagram is a particular choice of how to define this integral: it deforms the integral along the real axis to move into the complex plane and to pass just above the pole. With this definition the propagator becomes causal. (For t < t′ the integral can be completed by closing the contour in the upper half plane. The pole is not enclosed so Cauchy’s theorem says the contour integral vanishes. For t < t′ the integral can be completed by closing the contour in the upper half plane; Cauchy’s theorem says that the contour integral picks up the residue at the enclosed pole.)
Cauchy’s theorem can be applied because the pole lies either inside the contour (for t > t′) or outside the contour (for t < t′).
Yes ϵ > 0 for causality. Yes, it just a parameter for which we assume limϵ → 0. Take care: when ϵ goes to zero G(p,E,ϵ) = 1∕(E -p2∕2m + iϵ) has a real part that is (proportional to) a Dirac delta function and an imaginary part that is (proportional to) the Cauchy principal part of 1∕(E - p2∕2m). [See middle of page 81.]
This involves an expansion of the interaction energy to first order in (si-
s). The zeroth order term would be -(J∕2)∑
i,δs2, which is a constant
-(J∕2)N(2d)s2. The first order term would be -(J∕2)∑
i,δ2s ⋅ (si - s),
which is equal to -(J∕2)(2d)2∑
is ⋅ (si - s). (The second order term
is dropped.) Taking the zeroth and first order terms together gives: a
constant term, +JNds2 (not shown in the handout); a term that is linear
in si, given by -2Jd∑
isi⋅s, which is one of the terms given (with s = s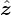 ).
The other term shown, linear in si, is just the coupling to B, as in the
initial H.
).
The other term shown, linear in si, is just the coupling to B, as in the
initial H.
For
H({si}) = ∑
i=1Nh(si), we can write exp(-βH) = ∏
i=1N exp(-βh(si)).
Then Z = ∑
{si}exp(-βH({si})) = ∏
i=1N![[∑ ]
si exp(- βh (si))](tp1_queries14x.png) . Since
all sites i are equivalent (h the same for them all), we can write this as
Z =
. Since
all sites i are equivalent (h the same for them all), we can write this as
Z = ![∑
[ sexp(- βh(s))]](tp1_queries15x.png) N. The integrals over θ and ϕ denote the sum over
all orientations of the classical vector s representing the spin.
N. The integrals over θ and ϕ denote the sum over
all orientations of the classical vector s representing the spin.
In computing ⟨si.z⟩, the same reasoning as above applies for all N -1 sites other than the site i on which you compute the average spin. For that one spin, you have an extra si.z = cosθ in the integral.
For a more detailed worked answer, see these notes.