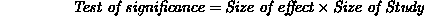
The so-called ``mind-body problem'' is arguably humankind's most enduring question. The crux of this question is whether mind can exist independently of the body. Or, to re-phrase it, is mind an epiphenomenon of brain functioning, or is it, to some degree, independent of the mechanistic properties of our physical brains? Throughout written history, the greatest philosophical thinkers have pondered this matter. However, outside of the field of parapsychology, there has been very little experimental research exploring whether consciousness can interact with its environment independently of the physical body. This paper will address these issues by exploring patterns found in experimental parapsychological research which suggest that mind or consciousness can interact directly with its environment without mediation by known physical mechanisms, e.g. senses, motor activity, physiological output. If the patterns emerging from this experimental work are as they appear, they may help shed some light on the ability of consciousness to act independently of the physical body.
Parapsychological research can broadly be conceptualised as addressing two main areas. The first of these, extrasensory perception (ESP), refers to the apparent obtaining of information by the mind without recourse to currently understood sensory means of gaining such information. The second area, psychokinesis (PK), refers to changes in physical systems apparently brought about by an act of conscious intention, without recourse to currently understood means of effecting such changes. Both ESP and PK can be conceptualised as anomalous interactions between mind and its environment, apparently not mediated by any currently understood physical, sensory means. Psi is a term used to refer to both ESP and PK phenomena.
This paper will present seven major meta-analyses carried out on various parapsychological databases. These seven were chosen as they demonstrate both ESP and PK research, and highlight the wide scope of psi experimentation which has been conducted over the last 60 years. Meta-analysis is a term which refers to a group of statistical procedures that are used to summarise and describe bodies of research. They provide a systematic means of combining results from groups of related individual studies to assess overall consistency of results, and can assist in identifying variables within the database that appear to affect outcomes, known as ``moderating variables''. Meta-analytic techniques provide quantitative, as opposed to qualitative, reviews of bodies of research. The term ``meta-analysis'' was first coined by Glass in 1976[1], although the basic procedures had been known for several decades (Snedecor [2]; Mosteller and Bush [3]). More recently, many books have been published detailing methods, procedures and theoretical considerations for conducting meta-analyses (e.g. Glass, McGaw and Smith [4]; Hedges and Olkin [5]; Wolf [6]; Hunter and Schmidt [7]; and Rosenthal [8]); these references will provide further details of the procedures and statistical formulae described generally below.
For readers who are unfamiliar with meta-analytic techniques, a brief summary of the basic components of meta-analysis will be given. After identifying a domain of study, all relevant studies are gathered together. The characteristics of those which are of interest are then coded, e.g. procedural variables and constants, study quality, etc. Ideally, this coding should be performed by one or more individuals who are not closely involved with the research topic, to avoid investigators' biases influencing any coding decisions. The statistical measures generated for each study (commonly referred to as ``test statistics'', e.g. z, t, chi-square, etc.) are converted into effect sizes. An effect size is a measure of the degree to which a phenomenon is present in the population (i.e., of how large the effect is). As noted by Rosenthal [8], commonly used statistical measures are usually a product how large the effect is and some function of the size of the study, often the square root of the number of trials or individuals. He expresses this (p. 20) as:
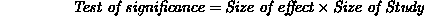
Most effect size measures are defined so that they are zero when the null hypothesis is true. Unlike ``test'' statistical measures, effect sizes do not grow in magnitude with the size of the study. Thus they provide a more accurate picture of replication across studies than can be provided by the standard statistical measures alone. This can be especially important when dealing with small effects and thus with studies with relatively low power, such as those commonly found in parapsychological research. Effect sizes allow studies to be assessed with a continuous measure, rather than the dichotomous measure to which test statistics are often reduced (i.e., statistically significant or not).
Replication across different studies is measured in terms of the consistency, or the ``homogeneity'' of the magnitude of the observed effect sizes. Again, this differs from the more traditional approach using test statistics, in which replication is defined by whether or not the null hypothesis is rejected in each study. Of course, when evaluating replication across a group of studies, confidence in any estimate of overall effect will be increased as the amount of confirming data increases. Using test statistics, outcomes from a group of studies can be combined and/or summarised to give an overall outcome for the database, weighting each study according to its size. In the following meta-analyses of parapsychological studies, the overall likelihood of observing the results if the null hypothesis is always true can be assessed by finding a combined z-score for all studies. This is simply a weighted average of the number of standard deviations the results deviated from chance, and its likelihood can be assessed using the standard statistical tables. One method of combining studies in this way is with a ``Stouffer z'' [3, 6, 9], and if the null hypotheses are always true, this statistic follows a standard normal curve. Stouffer's z provides a measure of how many standard deviations from chance the combined results of all of the studies fell. Using Stouffer's z, we can compute a `` p-value'' which gives us the probability of observing such extreme results if chance alone is the explanation. As we will see, the p-values for the meta-analyses in parapsychology are extremely low, thus effectively ruling out chance as an explanation for the data.
Using meta-analytic techniques, the impact of flaws upon study outcome and of various moderating variables can be quantitatively assessed, leading to improvements in study design and identification of factors associated with optimal outcomes. Possible relationships between variables can be recognised and tested in future experiments.
One problem that plagues all literature reviews is the tendency to report or publish only significant findings, commonly referred to as the ``file drawer problem''. However, there are a variety of methods available to estimate the size of the file drawer effect (i.e., the number of non-significant studies which would be required to nullify the outcome of a meta-analysis). For example, Rosenthal [8] provides a statistical measure, referred to as the ``Fail-Safe N'', to determine how many unpublished, null studies would be needed to negate an observed effect in any size of database, with the general guideline that a 5:1 ratio of null, unpublished studies to each published study should be obtained before the possibility of a negating file drawer effect can be safely eliminated.
In the following sections the findings of the selected meta-analyses will be presented. Consideration of possible interpretations, explanations and implications of this work will be found in the concluding Discussion section.