For consistency, one should apply the same prescription to all the
electrostatic interactions in the system, i.e. not only the
electron-electron terms, but also the electron-nucleus and nucleus-nucleus
interactions. These can be included by re-writing
Eq. (![]() ) to involve all charged particles as
) to involve all charged particles as
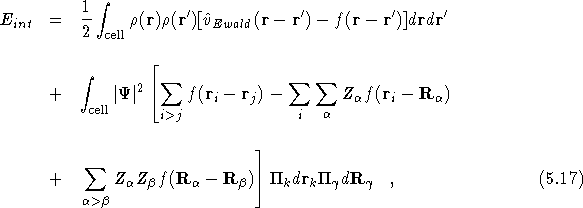
where ![]() is the many-body wavefunction for the electrons and
nuclei and
is the many-body wavefunction for the electrons and
nuclei and ![]() now also includes the charge density due to
the nuclei. In all our calculations we have made the adiabatic
approximation to separate the electronic and nuclear dynamical
variables
now also includes the charge density due to
the nuclei. In all our calculations we have made the adiabatic
approximation to separate the electronic and nuclear dynamical
variables
![]()
where the ![]() appear only as parameters in
appear only as parameters in ![]() . To
make further progress we must assume a form for the nuclear part of
the wavefunction,
. To
make further progress we must assume a form for the nuclear part of
the wavefunction, ![]() . The simplest assumption is that
. The simplest assumption is that ![]() can
be written as an appropriately symmetrised product of single-nucleus
functions which are very strongly localised and therefore
non-overlapping. The above equation then reduces to
can
be written as an appropriately symmetrised product of single-nucleus
functions which are very strongly localised and therefore
non-overlapping. The above equation then reduces to
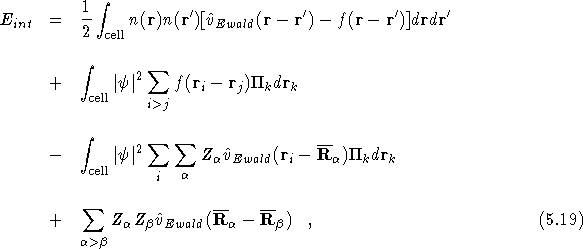
where the ![]() denote the centres of the
single-nucleus functions, and n is the electron density.
Note that the first two terms of the above equation correspond exactly
to the electron-electron interaction in Eq. (
denote the centres of the
single-nucleus functions, and n is the electron density.
Note that the first two terms of the above equation correspond exactly
to the electron-electron interaction in Eq. (![]() ), and
that the electron-nucleus and nucleus-nucleus terms now involve only
the Ewald interaction. The above result can be understood in the
following way. We are treating the ions as classical particles with
well defined positions and therefore expect no exchange-correlation
terms involving these particles. This leaves only the Hartree
interaction which is correctly described by the Ewald interaction. One
consequence of this is that as the Ewald interaction has a continuous
derivative, the forces on the ions are continuous functions of the
ionic positions, which means that this scheme is suitable for use in
quantum molecular dynamics calculations.
), and
that the electron-nucleus and nucleus-nucleus terms now involve only
the Ewald interaction. The above result can be understood in the
following way. We are treating the ions as classical particles with
well defined positions and therefore expect no exchange-correlation
terms involving these particles. This leaves only the Hartree
interaction which is correctly described by the Ewald interaction. One
consequence of this is that as the Ewald interaction has a continuous
derivative, the forces on the ions are continuous functions of the
ionic positions, which means that this scheme is suitable for use in
quantum molecular dynamics calculations.