


Next: Suggestions for Further
Up: Optimising the Trial
Previous: Adding a new
- The choice of is very important in determining both the energy
and variance of energy in a VMC calculation for solid germanium in the
diamond structure.
- The previously used form of ¸, based on a Fourier expansion of
2554
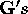 , whose coefficients were determined according to the method of
Fahy [9], did indeed produce an improved trial function,
, whose coefficients were determined according to the method of
Fahy [9], did indeed produce an improved trial function,
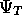 , compared with the
, compared with the 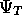 with no ¸. This can be seen in Figure
with no ¸. This can be seen in Figure
 . where the energy with no function in the trial
wavefunction is shown for comparison.
However, this method is extremely computationally
inefficient because 100-200
. where the energy with no function in the trial
wavefunction is shown for comparison.
However, this method is extremely computationally
inefficient because 100-200 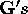 are adequate to describe ¸. The values
of the parameters being used were also far from optimal,
e.g the optimised value
for the first star of
are adequate to describe ¸. The values
of the parameters being used were also far from optimal,
e.g the optimised value
for the first star of 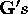 was 2 orders of magnitude greater than that
previously being used.
was 2 orders of magnitude greater than that
previously being used.
- Optimising the Fourier coefficients of by the minimisation of
variance scheme produces a with both a lower energy and variance of
energy than the unoptimised ¸. The function can be further
optimised by including an extra short range function, expressed as a
Chebyshev expansion, whose parameters are also optimised by minimisation
of variance.
- Even after fully optimising by the method described above, the
DMC energy is still 0.37 eV per atom lower than the VMC energy.
Attempts to lower this gap still further by improving the
Jastrow function in
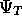 , by adding an additional short range function with
optimised coefficients, proved futile.
, by adding an additional short range function with
optimised coefficients, proved futile.
- Despite the fact that the whole optimisation procedure is based on
minimising the variance in the energy of a set of configurations, the
variance is only reduced by a small fraction in the above
optimisations.
Andrew Williamson
Mon May 22 14:48:37 BST 1995
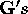 , whose coefficients were determined according to the method of
Fahy [9], did indeed produce an improved trial function,
, whose coefficients were determined according to the method of
Fahy [9], did indeed produce an improved trial function,
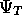 , compared with the
, compared with the 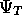 with no ¸. This can be seen in Figure
with no ¸. This can be seen in Figure
 . where the energy with no function in the trial
wavefunction is shown for comparison.
However, this method is extremely computationally
inefficient because 100-200
. where the energy with no function in the trial
wavefunction is shown for comparison.
However, this method is extremely computationally
inefficient because 100-200 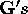 are adequate to describe ¸. The values
of the parameters being used were also far from optimal,
e.g the optimised value
for the first star of
are adequate to describe ¸. The values
of the parameters being used were also far from optimal,
e.g the optimised value
for the first star of 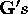 was 2 orders of magnitude greater than that
previously being used.
was 2 orders of magnitude greater than that
previously being used.
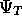 , by adding an additional short range function with
optimised coefficients, proved futile.
, by adding an additional short range function with
optimised coefficients, proved futile.


