Electron localization function
Formulation of electron localization function
The electron localization function (ELF) was introduced by Becke and Edgecombe as a "simple measure of electron localization in atomic and molecular systems" (Becke and Edgecombe, 1990). Becke and Edgecombe associated the localization of an electron with the probability density for finding a second like-spin electron near the reference point. For small probability densities, D(r) is also small and the electron is more localized.
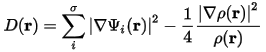
The Pauli repulsion between two like-spin electrons, described by the size of D(r), is taken as a measure of the electron localization. Using the corresponding factor found for a uniform electron gas, Dh(r), Becke and Edgecombe, defined ELF as:
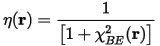
where
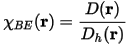
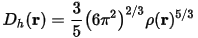
Becke and Edgecombe attributed the ratio χBE(r) to a dimensionless localization index, calibrated with respect to the uniform electron gas. This reference was chosen arbitrarily, so ELF is only a relative measure of the electron localization. High ELF values show that at the examined position the electrons are more localized than in a uniform electron gas of the same density. For example, when η(r) = 1/2 the effect of the Pauli repulsion is the same as in a uniform electron gas of the same density.
The ELF formulation originates from the Hartree-Fock description of electron gas. A formulation for ELF in DFT has been developed by Savin et al. (1992). This DFT-ELF approach evaluates the Pauli kinetic energy density based on the diagonal elements of the one-particle density matrix (the electron density). The Pauli kinetic energy is the energy due to the redistribution of the electrons in accordance with the Pauli principle and is the integral of the Pauli kinetic energy density:
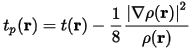
The Pauli kinetic energy density itself does not resolve the bonding situation. It is an arbitrary division of tP(r) by the kinetic energy density of a uniform electron gas of the same electron density, this yields all the information:
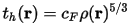
where cF is the Fermi constant:
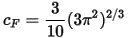
For a closed shell system the ratio:
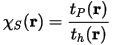
is formally identical to the ratio χBE(r) in the HF approximation. The same applies for an open shell system, where the kinetic energy densities are computed for the corresponding spin part only. So the ELF formulas based on χBE(r)) and χS(r) are identical. In the interpretation of Savin and coworkers (1992) ELF is a measure of the influence of Pauli principle as given by the Pauli kinetic energy density, relative to a uniform electron gas of the same density. Similarly, for the original definition ELF does not mirror tP(r).
How to interpret ELF
The values of ELF are fairly straightforward to calculate but may not be easy to interpret. The ELF website provides a very useful article on physical meanings of ELF and, in particular, on what ELF is not.
ELF was developed for all electron descriptions. ELF in CASTEP and ONETEP is calculated for valence electrons only, so it might be less meaningful. In particular, ELF values from CASTEP and ONETEP do not span the full range from 0 to 1. Extremely localized or delocalized electrons may be poorly described.