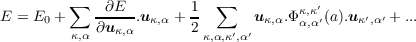
This guide introduces the concepts, keywords and techniques needed to set up and run CASTEP calculations of lattice dynamics and vibrational spectroscopy. The material covers the various lattice-dynamical and related methods implemented in CASTEP, how to set up a calculation, and presents simple examples of the major types of calculation. It is assumed that the reader is familiar with the general CASTEP input and output files and keywords to the level of, for example the tutorials on geometry optimisation which may be found at http://www.castep.org. It describes how to analyse the results and generate graphical output using the CASTEP tools, but does not cover the modelling of ir, raman or inelastic neutron or X-ray spectra, which are large subjects and beyond the scope of this document.
It does not describe the compilation and installation of CASTEP and its tools, nor does it describe the operational details of invoking and running CASTEP. Computational clusters, HPC computing environments and batch systems vary to a considerable degree, and the reader is referred to their cluster or computer centre documentation. It does discuss general aspects of managing and running large phonon calculations including restarts and parallelism in section 4.
There are many useful textbooks on the theory of vibrations in crystals, or lattice dynamics as the subject is usually known. A good beginner’s guide is “Introduction to Lattice Dynamics” by Martin Dove [2]. More advanced texts are available by Srivistava [3], Maradudin [4] and many others. The following section presents only a brief summary to introduce the notation.
Consider a crystal with a unit cell containing N atoms, labelled κ. The crystal is initially in mechanical equilibrium, with Cartesian co-ordinates Rκ,α, (α = 1..3 denotes the Cartesian x,y or z direction). uκ,α = xκ,α - Rκ,α denotes the displacement of an atom from its equilibrium position. Harmonic lattice dynamics is based on a Taylor expansion of total energy about structural equilibrium co-ordinates.
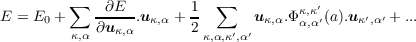 | (1.1) |
where uκ,α is the vector of atomic displacements from equilibrium and Φκ,κ′ α,α′ is the matrix of force constants
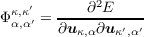 | (1.2) |
At equilibrium the forces Fκ,α = -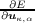 are all zero so the first-order term
vanishes. In the Harmonic Approximation the 3rd and higher order terms are
neglected1 .
Assume Born von Karman periodic boundary conditions and substitute a plane-wave guess for the
solution
are all zero so the first-order term
vanishes. In the Harmonic Approximation the 3rd and higher order terms are
neglected1 .
Assume Born von Karman periodic boundary conditions and substitute a plane-wave guess for the
solution
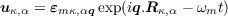 | (1.3) |
with a phonon wavevector q and a polarization vector εmκ,αq. This yields an eigenvalue equation
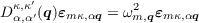 | (1.4) |
The dynamical matrix is defined as
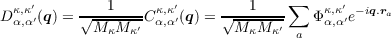 | (1.5) |
That is, the dynamical matrix is the mass-reduced Fourier transform of the force constant matrix.
The eigenvalue equation 1.4 can be solved by standard numerical methods. Dκ,κ′ α,α′(q) is Hermitian by construction. The vibrational frequencies at each mode are obtained as the square roots of the eigenvalues, and the eigenvectors give the pattern of atomic displacements belonging to each mode.
The central question of ab-initio lattice dynamics is therefore how to determine the force constants Φκ,κ′ α,α′ which are the second derivatives of the total energy with respect to two atomic displacements. The first derivatives are the forces, and may be determined straightforwardly using the Hellman-Feynmann Theorem by as the derivative of the quantum mechanical energy with respect to an atomic displacement, λ
If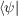 represents the ground state of Ĥ then the first two terms vanish because
represents the ground state of Ĥ then the first two terms vanish because 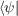 Ĥ
Ĥ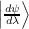 = ϵn
= ϵn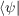
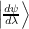 = 0.
Differentiating again yields
= 0.
Differentiating again yields
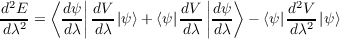 | (1.9) |
Unlike equation 1.8 the terms involving the derivatives of the wavefunctions do not vanish.
This means that it is necessary to somehow compute the electronic response of the system to
the displacement of an atom to perform ab-initio lattice dynamics calculations. This may
be accomplished either by a finite-displacement method, i.e. performing two calculations
which differ by a small displacement of an atomic co-ordinate and evaluating a numerical
derivative, or by using perturbation theory to evaluate the response wavefunction 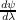 . (In
Kohn-Sham DFT, as implemented in CASTEP we actually evaluate the first-order response
orbitals.)
. (In
Kohn-Sham DFT, as implemented in CASTEP we actually evaluate the first-order response
orbitals.)
A good general reference on ab-initio lattice dynamics methods is the review paper by Baroni et al.[5].
A successful phonon calculation almost always consists of more than one stage, the usual sequence being a geometry optimisation followed by the phonon calculation itself. The importance of a high-quality structure optimisation can not be overemphasized - the energy expansion in lattice dynamics makes the explicit assumption that the system is in mechanical equilibrium and that all atomic forces are zero. (The only circumstance in which a geometry optimisation is unnecessary is a small, high symmetry system where all atoms lie on crystallographic high-symmetry positions and the forces are zero by symmetry.) It is not necessary to perform a variable-cell optimisation - the lattice dynamics is well defined at any stress or pressure, and phonons in high-pressure or strained systems are frequently of scientific interest. There is an excellent tutorial on geometry optimization at http://www.castep.org.
The requirement for a good geometry optimisation is sufficiently important that (as of release 5.0) prior to performing a phonon calculation CASTEP will compute the residual forces to determine if the geometry is converged. If any component of the force exceeds GEOM_FORCE_TOL it will print an error message and abort the run. Therefore any run following a successful geometry optimisation and using the correct final geometry and values of any convergence-related parameters should succeed. Should a run fail with this message, it may be because the geometry optimisation run did not in fact succeed, or because some parameter governing the convergence (e.g. the cutoff energy) differs in the phonon run compared to the geometry optimisation. In that case the correct procedure would be to re-optimise the geometry using the same parameters as needed for the phonon run. Alternatively if the geometry error and size of the force residual are tolerable, then the value of GEOM_FORCE_TOL may be increased in the .param file of the phonon calculation which will allow the run to proceed.
How accurate a geometry optimization is needed? Accumulated practical experience suggests that substantially tighter tolerances are needed to generate reasonable quality phonons than are needed for structural or energetics calculations. For many crystalline systems a geometry force convergence tolerance set using parameter GEOM_FORCE_TOL of 0.01 eV/Å is typically needed. For “soft” materials containing weak bonds such as molecular crystals or in the presence of hydrogen bonds, an even smaller value is frequently necessary. Only careful convergence testing of the geometry and resulting frequencies can determine the value to use. To achieve a high level of force convergence, it is obviously essential that the forces be evaluated to at least the same precision. This will in turn govern the choice of electronic k-point sampling, and probably require a smaller than default SCF convergence tolerance, ELEC_ENERGY_TOL. See section 2.8 for further discussion of geometry optimisation and convergence for phonon calculations.
If a lattice dynamics calculation is performed at the configuration which minimises the energy the force constant matrix Φκ,κ′ α,α′ is positive definite, and all of its eigenvalues are positive. Consequently the vibrational frequencies which are the square roots of the eigenvalues are real numbers. If on the other hand the system is not at a minimum energy equilibrium configuration Φκ,κ′ α,α′ is not necessarily positive definite, the eigenvalues may be negative. In that case the frequencies are imaginary and do not correspond to a physical vibrational mode. For convenience CASTEP prints such values using a a minus sign “-”. These are sometimes loosely referred to as “negative” frequencies, but bear in mind that this convention really indicates negative eigenvalues and imaginary frequencies.2
CASTEP lattice dynamics uses symmetry to reduce the number of perturbation calculations to the irreducible set, and applies the symmetry transformations to generate the full dynamical matrix. Combined with the usual reduction in k-points in the IBZ, savings in CPU time by use of symmetry can easily be a factor of 10 or more. It is therefore important to maximise the symmetry available to the calculation, and to either specify the symmetry operations in the .cell file using the %BLOCK SYMMETRY_OPS keyword or generate them using SYMMETRY_GENERATE.
CASTEP generates the dynamical matrix using perturbations along Cartesian X, Y and Z directions. To maximise the use of symmetry and minimise the number of perturbations required, the symmetry axes of the crystal or molecule should be aligned along Cartesian X, Y, and Z. If the cell axes are specified using %BLOCK LATTICE_ABC CASTEP attempts to optimally orient the cell in many cases, but if using %BLOCK LATTICE_CART it is the responsibility of the user. This is one of the few cases where the absolute orientation makes any difference in a CASTEP calculation. An optimal orientation will use the fewest perturbations and lowest CPU time and will also exhibit best convergence with respect to, for example electronic k-point set.
There is a further consideration related to symmetry; structure, cell and atomic co-ordinates must be specified to a reasonably high accuracy in the input files. CASTEP uses stochastic methods to analyse the effect of symmetry operations on the dynamical matrix, and this analysis can fail to detect symmetries or otherwise misbehave unless symmetry operations, lattice vectors and atomic co-ordinates are consistent to a reasonable degree of precision. It is recommended that symmetry-related lattice vectors and internal co-ordinates are consistent to at least 10-6Å which can only be achieved if the values in the .cell file are expressed to this number of decimal places. This is particularly significant in the case of trigonal or hexagonal systems specified with %BLOCK LATTICE_CART where equality of the a and b cell vector lengths is only as precise as the number of significant figures used to represent the components.
As of version 5.0 CASTEP gained a cell file keyword
which will adjust co-ordinates and vectors to satisfy symmetry to high precision.
Alternatively there is a utility program in the academic distribution named symmetry_snap which implements the same functionality. This is invoked simply as
symmetry_snap seedname
which reads seedname.cell and outputs the symmetrised version to seedname-symm.cell